题目内容
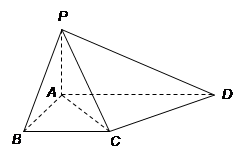
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB, PC的中点 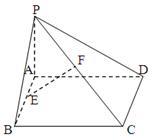
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°,求EF与平面ABCD所成的角的大小.
(1)∵ABCD是矩形,取PB的中点为G,连GF,GE,证得平面GEF//平面PAD,EF∥平面PAD。(2)证明△PAE≌△CBE,得出EF⊥PC。又CD⊥GE证得CD⊥平面GEF,推出EF⊥CD。
(3)EF与面ABCD所成的角为45°。
解析试题分析:(1)∵ABCD是矩形,取PB的中点为G,连GF,GE,由三角形中位线定理,知GF//BC//AD,GE//PA,又GE与GF交于G,PA与AD交于A,所以平面GEF//平面PAD,EF∥平面PAD。
(2)∵ABCD是矩形,∴CB=AD、∠CBE=90°、BC⊥CD。
∵PA⊥平面ABCD,∴∠PAE=90°。
∵PA=AD、CB=AD,∴PA=CB,又AE=BE、∠PAE=∠CBE=90°,∴△PAE≌△CBE,
∴CE=PE,而F∈PC且PF=CF,∴EF⊥PC。
∵G、F分别是PB、PC的中点,∴GF是△PBC的中位线,∴GF∥BC,而BC⊥CD,
∴CD⊥GF。
∵G、E分别是PB、AB的中点,∴GE是△BPA的中位线,∴GE∥PA,而PA⊥平面ABCD,
∴GE⊥平面ABCD,∴CD⊥GE。
由CD⊥GF、CD⊥GE、GF∩GF=G,∴CD⊥平面GEF,∴EF⊥CD。
(3)过F作FO⊥AC交AC于O。
∵PA⊥面ABCD,∴PA⊥AC,PA⊥EO,得:FO∥PA,FO⊥EO,AO=CO。
由PF=CF,FO∥PA,得:FO=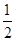 PA。
PA。
由AE=BE,AO=CO,得:EO=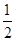 BC。
BC。
由PA⊥面ABCD,FO∥PA,得:FO⊥面ABCD,∴∠FEO就是EF与面ABCD所成的角。
∵PA⊥面ABCD,∴PA⊥AD,又∠PDA=45°,∴PA=AD,结合证得的FO=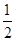 PA,
PA,
得:FO=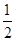 AD。
AD。
∵ABCD是矩形,∴AD=BC,结合证得的EO=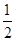 BC,得:EO=
BC,得:EO=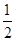 AD。
AD。
由FO=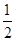 AD,EO=
AD,EO=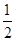 AD,FO⊥EO,得:∠FEO=45°。
AD,FO⊥EO,得:∠FEO=45°。
即:EF与面ABCD所成的角为45°。
考点:本题主要考查立体几何中的平行关系、垂直关系,角的计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。

 阅读快车系列答案
阅读快车系列答案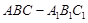 中,
中,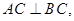
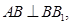
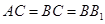 ,
,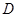 为
为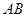 的中点,且
的中点,且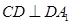 .
.
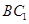 ∥平面
∥平面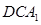 ;
;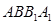 所成角的大小.
所成角的大小.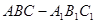 中,
中,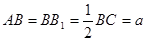 ,
,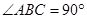 ,
,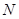 、
、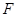 分别为
分别为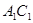 、
、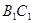 的中点.
的中点.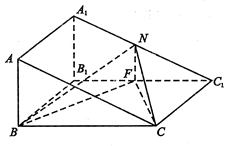
 平面
平面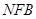 ;
;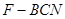 的体积.
的体积.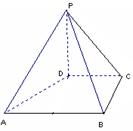
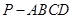 的底面是正方形,
的底面是正方形,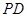 ⊥底面
⊥底面 ,点
,点 在棱
在棱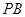 上.
上.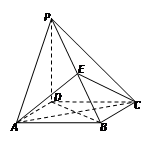
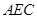 ⊥平面
⊥平面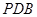 ;
;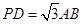 且
且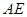 与平面
与平面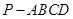 中,底面
中,底面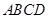 为直角梯形,且
为直角梯形,且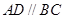 ,
, ,侧面
,侧面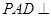 底面
底面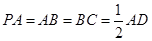 .
.
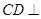 平面
平面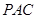 ;
;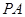 上是否存在点
上是否存在点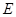 ,使得
,使得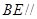 平面
平面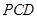 ?若存在,指出点
?若存在,指出点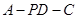 的余弦值.
的余弦值. 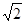
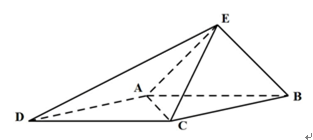

 ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值. 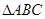 中,点
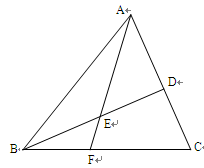
中,点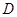 是
是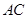 的中点,点
的中点,点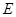 是
是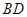 的中点,
的中点,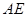 的延长线交
的延长线交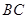 与点
与点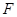 。
。
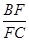 的值;
的值;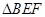 的面积为
的面积为 ,四边形
,四边形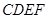 的面积为
的面积为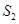 ,求
,求 的值。
的值。