题目内容
如图,四棱锥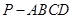 的底面是正方形,
的底面是正方形,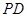 ⊥底面
⊥底面 ,点
,点 在棱
在棱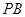 上.
上.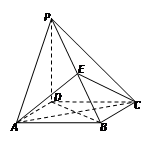
(1)求证:平面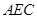 ⊥平面
⊥平面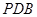 ;
;
(2)当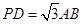 且
且 为
为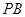 的中点时,求
的中点时,求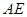 与平面
与平面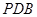 所成角的正弦值.
所成角的正弦值.
(Ⅰ)利用线面垂直证明面面垂直;(Ⅱ) 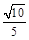 .
.
解析试题分析:(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,
∵PD⊥底面ABCD,∴PD⊥AC,∴AC⊥平面PDB,
又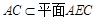 ,∴平面AEC⊥平面PDB. (6分)
,∴平面AEC⊥平面PDB. (6分)
(Ⅱ)方法一:如图1,设AC∩BD=O,连接OE, 
由(Ⅰ)知AC⊥平面PDB于O,∴∠AEO为AE与平面PDB所成的角,
∵O,E分别为DB、PB的中点,∴OE∥PD,且OE= PD,
PD,
又∵PD⊥底面ABCD, ∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中,由PD= AB,
AB,
设 ,则
,则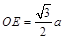 ,
, ,∴
,∴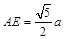 ,于是
,于是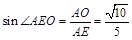 ,
,
即AE与平面PDB所成角的正弦值为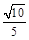 . (12分)
. (12分)
方法二:如图2,以D为原点建立空间直角坐标系D?xyz,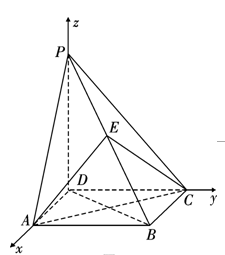
设 ,AE与平面PDB所成的角为
,AE与平面PDB所成的角为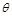 ,
,
则 ,
, ,
, ,
, ,
,
于是 ,所以
,所以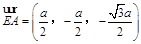 ,
,
且平面 的法向量
的法向量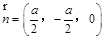 ,所以
,所以 ,
,
即AE与平面PDB所成角的正弦值为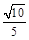 . (12分)
. (12分)
考点:本题考查了空间中的线面关系及空间角的求法
点评:直线和平面成角的重点是研究斜线和平面成角,常规求解是采用“作、证、算”,但角不易作出时,可利用构成三条线段的本质特征求解,即分别求斜线段、射影线段、点A到平面的距离求之.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
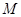 ,
, 分别是
分别是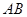 ,
, 的中点.
的中点.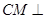 平面
平面 ;
;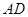 上(含
上(含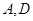 端点)确定一点
端点)确定一点 ,使得
,使得 ∥平面
∥平面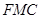 ,并给出证明.
,并给出证明.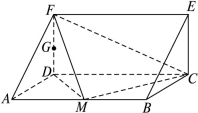


 中,
中, 点
点 在棱
在棱 上.
上.
 与
与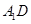 所成的角;
所成的角; 的大小为
的大小为 ,求点
,求点 到面
到面 的距离.
的距离. ,在直线DE上是否存在一点
,在直线DE上是否存在一点 ,使得
,使得 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点

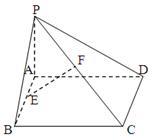
 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
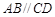 ,
,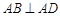 ,且
,且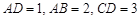 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且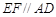 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.
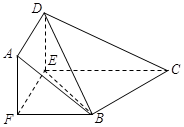
 平面BDE;
平面BDE; 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点

 的平面角的余弦值.
的平面角的余弦值.