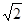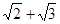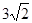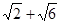题目内容
长方体ABCD-A1B1C1D1中,∠DAD1=45°,∠CAC1=30°那么异面直线AD1与DC1所成角
是
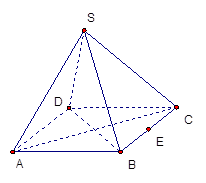
A. | B.2 | C. | D. |
C
解析试题分析:在长方体中,由于∠DAD1=45°,∠CAC1=30°将AD1平移到BC1,然后将所求的角转化为BC1与DC1所成角,那么只要确定了长方体的边长即可得到结论,设底面的高为1,底面边AD=1,AC1=2,AC=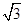 ,那么BC1
,那么BC1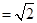 ,AB=
,AB=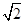 ,结合三角形的余弦定理可知BC1与DC1所成角的正弦值为
,结合三角形的余弦定理可知BC1与DC1所成角的正弦值为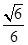 ,那么可知该角为选项C.
,那么可知该角为选项C.
考点:本试题考查了空间中异面直线所成的角的知识。
点评:解决该试题的关键是对于异面直线的角转化为同一平面内的角来求解处理,采用的方法是平移法,经常用中位线平移,或者是平行四边形的性质来平移得到角的表示,进而得到结论。

练习册系列答案
相关题目
从正方体的八个顶点中任取四个点连线,在能构成的一对异面直线中,其所成的角的度数不可能是
| A.30° | B.45° | C.60° | D.90° |
设 ,
, 是两条不同的直线,
是两条不同的直线,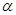 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
设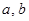 是两条直线,
是两条直线,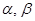 是两个不同平面,下列四个命题中,正确的命题是
是两个不同平面,下列四个命题中,正确的命题是
A.若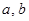 与 与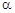 所成的角相等,则 所成的角相等,则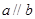 |
B.若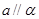 , ,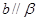 , ,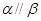 ,则 ,则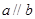 |
C.若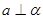 , ,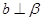 , ,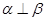 ,则 ,则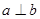 |
D.若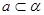 , ,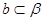 , ,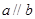 ,则 ,则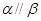 |
如图,在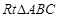 中,
中,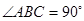 ,
,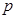 为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为
为△ABC所在平面外一点,PA⊥面ABC,则四面体P-ABC中共有直角三角形个数为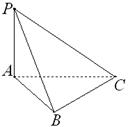
| A.4 | B.3 | C.2 | D.1 |
如果对于空间任意n(n≥2)条直线总存在一个平面α,使得这n条直线与平面α所成的角均相等,那么这样的n( )
| A.最大值为3 | B.最大值为4 | C.最大值为5 | D.不存在最大值 |
二面角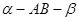 的平面角是锐角,点C
的平面角是锐角,点C 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面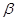 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
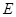 是
是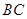 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持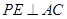 .则动点
.则动点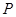 的轨迹与△
的轨迹与△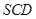 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )
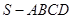 的底面边长为2,高为2,
的底面边长为2,高为2,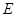 为边
为边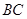 的中点,动点
的中点,动点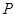 在表面上运动,并且总保持
在表面上运动,并且总保持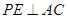 ,则动点
,则动点