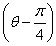题目内容
已知a，b，m，n均为正数，且a＋b＝1，mn＝2，则(am＋bn)·(bm＋an)的最小值为________．
2.
【解析】∵a，b，m，n∈R＋，且a＋b＝1，mn＝2，
∴(am＋bn)( bm＋an)＝abm2＋a2mn＋b2mn＋abn2＝ab(m2＋n2)＋2(a2＋b2)≥2ab·mn＋2(a2＋b2)
＝4ab＋2(a2＋b2)＝2(a2＋b2＋2ab)＝2(a＋b)2＝2，
当且仅当m＝n＝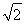
时，取“＝”．
∴所求最小值为2.
练习册系列答案
阅读快车系列答案
相关题目
