题目内容
定义在R上的函数f(x)=-x-x3,设x1+x2≤0,下列不等式中正确的序号有 .
①f(x1)f(-x1)≤0 ②f(x2)f(-x2)>0
③f(x1)+f(x2)≤f(-x1)+f(-x2) ④f(x1)+f(x2)≥f(-x1)+f(-x2)
①④
解析试题分析:解:f(x)f(-x)=(-x-x3)(x+x3)=-(x+x3)2≤0,所以①正确,②不正确.易知f(x)是R上的减函数,由x1+x2≤0,知x1≤-x2,x2≤-x1,
∴f(x1)≥f(-x2),f(x2)≥f(-x1).∴f(x1)+f(x2)≥f(-x1)+f(-x2),故④正确.8因此正确的答案为①④
考点:函数单调性
点评:解决的关键是利用函数的单调性的定义来求解,属于基础题。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 仅有一解,则实数
仅有一解,则实数 的取值范围是 .
的取值范围是 .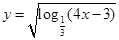 的定义域为 .
的定义域为 . 的值域为 .
的值域为 . 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当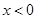 时,
时, ,则当
,则当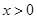 时,
时,  = .
= . 的解所在区间为
的解所在区间为 ,则
,则 = .
= . 和函数
和函数 的图像关于直线
的图像关于直线 对称,
对称, ,则
,则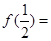
 的最大值为M,最小值为N,那么M+N= _________ .
的最大值为M,最小值为N,那么M+N= _________ .