题目内容
设公差不为0的等差数列{an}的前n项和为Sn,a1=2,且a1,a3,a7成等比数列.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn=
,求数列{bn}的前n项和Tn.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn=
| 2n+1Sn | n+3 |
分析:(I)由已知可得,a32=a1a7,利用等差数列的通项公式及已知可求公差d,进而可求通项
(II)由(I)可知,Sn=
,进而可得bn=n•2n,利用错位相减可求数列的和
(II)由(I)可知,Sn=
| n(n+3) |
| 2 |
解答:解:(I)设数列{an}的公差为d
∵a1,a3,a7成等比数列
∴a32=a1a7
∴(a1+2d)2=a1•(a1+6d)
∵a1=2
∴d=1或d=0(舍去)
∴an=2+(n-1)•1=n+1
(II)由(I)可知,Sn=
∴bn=n•2n
∴Tn=1•2+2•22+3•23+…+n•2n
∴2Tn=1•22+2•23+3•24+…+n•2n+1
两式相减可得,-Tn=2+22+23+…+2n-n.2n+1
=
-n•2n+1
∴Tn=(n-1)•2n+1+2
∵a1,a3,a7成等比数列
∴a32=a1a7
∴(a1+2d)2=a1•(a1+6d)
∵a1=2
∴d=1或d=0(舍去)
∴an=2+(n-1)•1=n+1
(II)由(I)可知,Sn=
| n(n+3) |
| 2 |
∴bn=n•2n
∴Tn=1•2+2•22+3•23+…+n•2n
∴2Tn=1•22+2•23+3•24+…+n•2n+1
两式相减可得,-Tn=2+22+23+…+2n-n.2n+1
=
| 2(1-2n) |
| 1-2 |
∴Tn=(n-1)•2n+1+2
点评:本题主要考查了等差数列与等比 数列的基本运算,数列求和的错位相减求和方法的应用是解答本题的关键

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
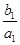 +
+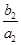 +…+
+…+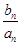 =1-
=1-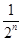 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.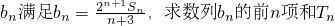 .
.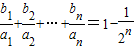 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.