题目内容
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)设![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1) ![]() .
.
(2) 故x=±![]() 时,g(x)取得最大值-3.
时,g(x)取得最大值-3.
【解析】分析:(1)不等式![]() 等价于
等价于![]() ,两边平方后利用一元二次不等式的解法求解即可;(2)将
,两边平方后利用一元二次不等式的解法求解即可;(2)将![]() ,写成分段函数形式,利用函数的单调性,可得当
,写成分段函数形式,利用函数的单调性,可得当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
详解:(1)由题意得|x-1|≥|2x-3|,
所以|x-1|2≥|2x-3|2
整理可得3x2-10x+8≤0,解得![]() ≤x≤2,
≤x≤2,
故原不等式的解集为{x|![]() ≤x≤2}.
≤x≤2}.
(2)显然g(x)=f(x)+f(-x)为偶函数,
所以只研究x≥0时g(x)的最大值.
g(x)=f(x)+f(-x)=|x-1|-|2x-3|+|x+1|-|2x+3|,
所以x≥0时,g(x)=|x-1|-|2x-3|-x-2
=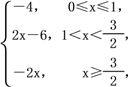
所以当x=![]() 时,g(x)取得最大值-3,
时,g(x)取得最大值-3,
故x=±![]() 时,g(x)取得最大值-3.
时,g(x)取得最大值-3.

【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表如下,从该校随机选取一名学生,则估计这名学生该周课外阅读时间少于12小时的概率为__________.
组号 | 分组 | 频数 |
1 | [0,2) | 6 |
2 | [2,4) | 8 |
3 | [4,6) | 17 |
4 | [6,8) | 22 |
5 | [8,10) | 25 |
6 | [10,12) | 12 |
7 | [12,14) | 6 |
8 | [14,16) | 2 |
9 | [16,18) | 2 |
合计 | 100 | |
【题目】小明某天偶然发现班上男同学比女同学更喜欢做几何题,为了验证这一现象是否具有普遍性,他决定在学校开展调查研究:他在全校3000名同学中随机抽取了50名,给这50名同学同等难度的几何题和代数题各一道,让同学们自由选择其中一道题作答,选题人数如下表所示,但因不小心将部分数据损毁,只是记得女生选择几何题的频率是![]() .
.
几何题 | 代数题 | 合计 | |
男同学 | 22 | 8 | 30 |
女同学 | |||
合计 |
(1)根据题目信息补全上表;
(2)能否根据这个调查数据判断有![]() 的把握认为选代数题还是几何题与性别有关?
的把握认为选代数题还是几何题与性别有关?
参考数据和公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | p>5.024 | 6.635 | 7.879 |
 ,其中
,其中![]() .
.
【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以
条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.如表是本市一主干路段监控设备所抓拍的
分的行政处罚.如表是本市一主干路段监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(Ⅰ)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)预测该路段![]() 月份的不“礼让斑马线”违章驾驶员人数.
月份的不“礼让斑马线”违章驾驶员人数.
参考公式: ,
,![]() .
.