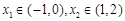题目内容
已知函数 ,
, 
(Ⅰ)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅱ)令 ,是否存在实数
,是否存在实数 ,当
,当
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(III)当
 时,证明:
时,证明: 
 ,
, 
(Ⅰ)若函数
 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;(Ⅱ)令
 ,是否存在实数
,是否存在实数 ,当
,当
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;(III)当

 时,证明:
时,证明: 
(Ⅰ) (Ⅱ)
(Ⅱ) ,使得当
,使得当 时
时 有最小值3(III)见解析
有最小值3(III)见解析
 (Ⅱ)
(Ⅱ) ,使得当
,使得当 时
时 有最小值3(III)见解析
有最小值3(III)见解析本试题主要是考查了运用导数研究函数的最值的问题以及函数单调性的综合运用。
(1)要是函数在给定区间递减,则导函数在此区间上恒小于等于零,分离参数的思想得到参数的范围。
(2)假设存在实数a,那么根据对于参数的讨论得到最值。
解:(Ⅰ) 在
在 上恒成立,
上恒成立,
令 ,有
,有 得
得 得
得 .
.
方法二: 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,令
上恒成立,令 ,而
,而 在
在 上单调递减,
上单调递减,
\
(Ⅱ)假设存在实数 ,使
,使 (
( )有最小值3,
)有最小值3,


①当 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),
②当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增

 ,
, ,满足条件.
,满足条件.
③当 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),
综上,存在实数 ,使得当
,使得当 时
时 有最小值3.
有最小值3.
(III)令 ,由(2)知,
,由(2)知, .令
.令 ,
, ,
,
当 时,
时, ,
, 在
在 上单调递增
上单调递增
∴

即

(1)要是函数在给定区间递减,则导函数在此区间上恒小于等于零,分离参数的思想得到参数的范围。
(2)假设存在实数a,那么根据对于参数的讨论得到最值。
解:(Ⅰ)
 在
在 上恒成立,
上恒成立,令
 ,有
,有 得
得 得
得 .
.方法二:
 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,令
上恒成立,令 ,而
,而 在
在 上单调递减,
上单调递减,
\

(Ⅱ)假设存在实数
 ,使
,使 (
( )有最小值3,
)有最小值3,

①当
 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),②当
 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
 ,
, ,满足条件.
,满足条件. ③当
 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),综上,存在实数
 ,使得当
,使得当 时
时 有最小值3.
有最小值3. (III)令
 ,由(2)知,
,由(2)知, .令
.令 ,
, ,
,当
 时,
时, ,
, 在
在 上单调递增
上单调递增 ∴


即



练习册系列答案
相关题目
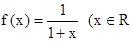 且
且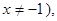
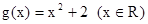 。
。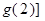 的值;
的值;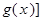 和g[
和g[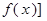 的解析式。
的解析式。 (其中
(其中 为常数).某人用(0,0),(10,1.1),(30,6.9)求出相关系数,用(60,24.8)验证,请问用以上哪个函数作为模拟函数较好,并说明理由.在一次由这种型号的汽车发生的交通事故中,测得刹车距离为14.4m,问汽车在刹车时的速度大概是多少?
为常数).某人用(0,0),(10,1.1),(30,6.9)求出相关系数,用(60,24.8)验证,请问用以上哪个函数作为模拟函数较好,并说明理由.在一次由这种型号的汽车发生的交通事故中,测得刹车距离为14.4m,问汽车在刹车时的速度大概是多少? ,且
,且 )
)
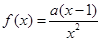 ,其中
,其中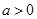 。
。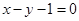 是曲线
是曲线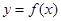 的切线,求a的值;
的切线,求a的值;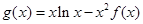 ,求
,求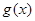 在区间
在区间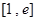 上的最大值。(其中e为自然对数的底数)。
上的最大值。(其中e为自然对数的底数)。 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤ 中,满足条件“
中,满足条件“ ”的有 .
”的有 . ,那么
,那么 ______
______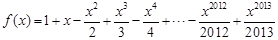 ,
,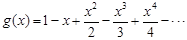
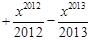 ,若函数
,若函数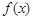 有唯一零点
有唯一零点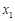 ,函数
,函数 有唯一零点
有唯一零点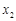 ,则有( )
,则有( )