题目内容
设a是整数，0≤b＜1．若a2＝2b(a＋b)，则b＝ ．
0，，－1．
：若a为负整数，则a2＞0，2b(a＋b)＜0，不可能，故a≥0．
于是a2＝2b(a＋b)＜2(a＋1)Þa2－2a－2＜0Þ0≤a＜1＋Þa＝0，1，2．
a＝0时，b＝0；a＝1时，2b2＋2b－1＝0Þb＝；a＝2时，b2＋2b－2＝0Þb＝－1．
说明：本题也可以这样说：求实数x，使[x]2＝2{x}x．
于是a2＝2b(a＋b)＜2(a＋1)Þa2－2a－2＜0Þ0≤a＜1＋Þa＝0，1，2．
a＝0时，b＝0；a＝1时，2b2＋2b－1＝0Þb＝；a＝2时，b2＋2b－2＝0Þb＝－1．
说明：本题也可以这样说：求实数x，使[x]2＝2{x}x．
练习册系列答案
相关题目
x2+2x＞mx的解集为{x|0＜x＜2}，则实数m的值为_______.
的解集为
，求实数p与q的值．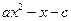
＞0的解集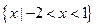
，则函数y＝f（－x）的图象为（ ）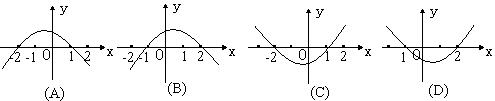
的不等式
的解集是
， 求不等式
的解集。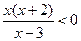
的解集是为 .