题目内容
已知函数
(1)若不等式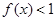 的解集为
的解集为 ,求
,求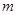 的取值范围;
的取值范围;
(2)解关于 的不等式
的不等式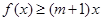 ;
;
(3)若不等式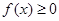 对一切
对一切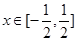 恒成立,求
恒成立,求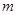 的取值范围.
的取值范围.
【答案】
(1)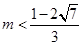 ,(2)①当
,(2)①当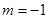 时,解集为
时,解集为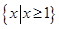 ;②当
;②当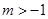 时,解集为
时,解集为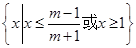 ;③当
;③当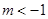 时,解集为R;(3)
时,解集为R;(3)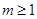
【解析】
试题分析:(1)①当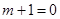 即
即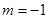 时,
时,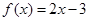 ,不合题意; 1分
,不合题意; 1分
②当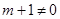 即
即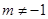 时,
时,
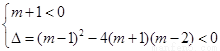 ,即
,即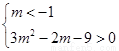 ,
3分
,
3分
∴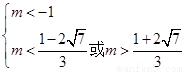 ,∴
,∴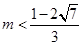 5分
5分
(2)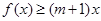 即
即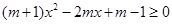
即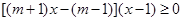
①当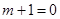 即
即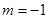 时,解集为
时,解集为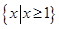 7分
7分
②当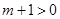 即
即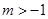 时,
时,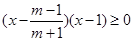
∵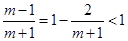 ,∴解集为
,∴解集为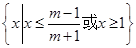 9分
9分
③当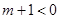 即
即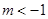 时,
时,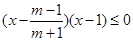
∵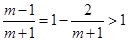 ,∴解集为R 11分
,∴解集为R 11分
(3)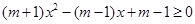 ,即
,即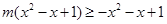 ,
,
∵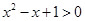 恒成立,∴
恒成立,∴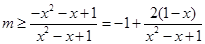 13分
13分
设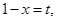 则
则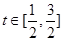 ,
,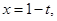
∴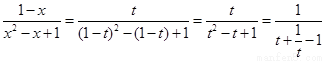 ,
,
∵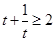 ,当且仅当
,当且仅当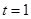 时取等号,∴
时取等号,∴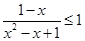 ,当且仅当
,当且仅当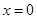 时取等号,
时取等号,
∴当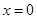 时,
时,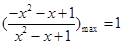 ,∴
,∴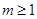 16分
16分
考点:本题考查了含参一元二次不等式的的解法及恒成立问题
点评:在解关于含参数的一元二次不等式时,往往都要对参数进行分类讨论.为了要做到分类“不重不漏”,讨论时需注意分类的标准.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
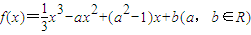

 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.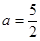 且关于
且关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 满足:
满足: 求证:
求证:

 恒成立,求实数
恒成立,求实数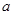 的最小值.
的最小值. 且关于
且关于 的方程
的方程 在
在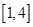 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 满足:
满足: 求证:
求证:
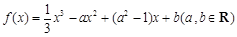
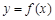 的图象在点
的图象在点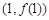 处的切线方程为
处的切线方程为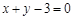 ,求
,求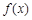 在区间
在区间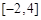 上的最大值;
上的最大值;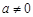 时,若
时,若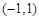 上不单调,求
上不单调,求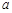 的取值范围.
的取值范围.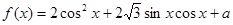 .
.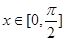 且
且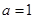 时,求
时,求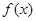 的最大值和最小值,以及取得最大值和最小值时
的最大值和最小值,以及取得最大值和最小值时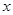 的
的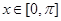 且
且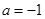 时,方程
时,方程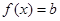 有两个不相等的实数根
有两个不相等的实数根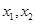 ,求
,求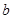 的取值
的取值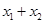 的值.
的值.