题目内容
已知函数
(1)若对任意的 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
(2)若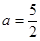 且关于
且关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)设各项为正的数列 满足:
满足: 求证:
求证:
【答案】
(1) ; (2)
; (2)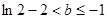 ; (3)
; (3)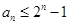
【解析】
试题分析:(I)依题意,对任意的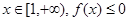 恒成立,即
恒成立,即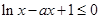 在x
在x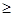 1恒成立.则a
1恒成立.则a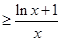 .
.
而
 0,所以,
0,所以,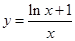 在
在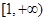 是减函数,
是减函数,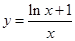 最大值为1,所以,
最大值为1,所以,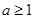 ,实数
,实数 的最小值。
的最小值。
(II)因为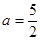 ,且
,且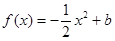 在
在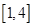 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
即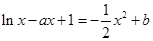 在
在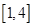 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
设g(x)=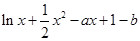 ,则g'(x)=
,则g'(x)=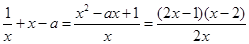
列表:
|
X |
(0, |
|
( |
2 |
(2,4) |
|
|
+ |
0 |
- |
0 |
+ |
|
|
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以,g(x)极大值=g(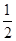 )=
)= -ln2-b,g(x)极大值=g(2)=ln2-b-2,
-ln2-b,g(x)极大值=g(2)=ln2-b-2,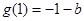 ,g(4)=2ln2-b-1
,g(4)=2ln2-b-1
因为,方程g(x)=0在[1,4]上恰有两个不相等的实数根.
则 ,解得
,解得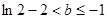 .
.
(III)设h(x)=lnx-x+1,x∈[1,+∞),则h'(x)= -1≤0
-1≤0
∴h(x)在[1,+∞)为减函数,且h(x)max=h(1)=0,故当x≥1时有lnx≤x-1.
∵a1=1,假设ak≥1(k∈N*),则ak+1=lnak+ak+2>1,故an≥1(n∈N*)
从而an+1=lnan+an+2≤2an+1∴1+an+1≤2(1+an)≤…≤2n(1+a1)
即1+an≤2n,∴an≤2n-1
考点:本题主要考查应用导数研究函数的单调性及极(最)值,研究函数的图象和性质,数列不等式的证明。
点评:难题,不等式恒成立问题,常常转化成求函数的最值问题。(II)(III)两小题,均是通过构造函数,研究函数的单调性、极值(最值),认识函数图象的变化形态等,寻求得到解题途径。有一定技巧性,对学生要求较高。

练习册系列答案
相关题目
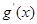
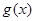

 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。 在区间
在区间 上的最小值
上的最小值 的表达式。
的表达式。
 恒成立,求实数
恒成立,求实数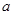 的最小值.
的最小值. 且关于
且关于 的方程
的方程 在
在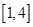 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 满足:
满足: 求证:
求证:
 .
.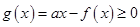 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 有且仅有三个公共点,且公共点的横坐标的最大值为
有且仅有三个公共点,且公共点的横坐标的最大值为 ,求证:
,求证: .
. .
. ,都有
,都有 ,求
,求 的取值范围;
的取值范围; 时,
时,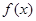 的最大值为M,求证:
的最大值为M,求证: ;
; ,求证:对于任意的
,求证:对于任意的 的充要条件是
的充要条件是