题目内容
已知函数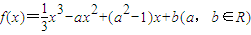
(1)若y=f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0,求f(x)在区间[-2,4]上的最大值;
(2)当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围.
【答案】分析:(1)先求f(1),利用(1,f(1))在y=f(x)上,及f'(1)=-1,建立方程,即可求得函数解析式,进而可得函数的极值,利用函数的最值在极值与端点处取得,可得结论;
(2)因为函数f(x)在区间(-1,1)不单调,所以函数f'(x)在(-1,1)上存在零点,利用f'(-1)f'(1)<0,即可求得a的取值范围.
解答:解:(1)∵(1,f(1))在x+y-3=0上,∴f(1)=2
∵(1,2)在y=f(x)上,
∴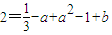
又f'(1)=-1,∴1-2a+a2-1=-1
∴a2-2a+1=0,解得
∴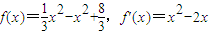
由f'(x)=0可知x=0和x=2是f(x)的极值点.
∵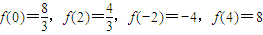
∴f(x)在区间[-2,4]上的最大值为8.
(2)因为函数f(x)在区间(-1,1)不单调,所以函数f'(x)在(-1,1)上存在零点.
而f'(x)=0的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点.
所以f'(-1)f'(1)<0,即a2(a+2)(a-2)<0.
∵a2>0,∴(a+2)(a-2)<0,-2<a<2.
又∵a≠0,
∴a∈(-2,0)∪(0,2).
点评:本题考查导数知识的运用,考查函数的最值,考查函数的单调性,考查学生分析解决问题的能力,函数f(x)在区间(-1,1)不单调,转化为函数f'(x)在(-1,1)上存在零点是解题的关键.
(2)因为函数f(x)在区间(-1,1)不单调,所以函数f'(x)在(-1,1)上存在零点,利用f'(-1)f'(1)<0,即可求得a的取值范围.
解答:解:(1)∵(1,f(1))在x+y-3=0上,∴f(1)=2
∵(1,2)在y=f(x)上,
∴
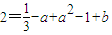
又f'(1)=-1,∴1-2a+a2-1=-1
∴a2-2a+1=0,解得

∴
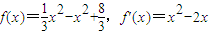
由f'(x)=0可知x=0和x=2是f(x)的极值点.
∵
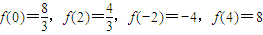
∴f(x)在区间[-2,4]上的最大值为8.
(2)因为函数f(x)在区间(-1,1)不单调,所以函数f'(x)在(-1,1)上存在零点.
而f'(x)=0的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点.
所以f'(-1)f'(1)<0,即a2(a+2)(a-2)<0.
∵a2>0,∴(a+2)(a-2)<0,-2<a<2.
又∵a≠0,
∴a∈(-2,0)∪(0,2).
点评:本题考查导数知识的运用,考查函数的最值,考查函数的单调性,考查学生分析解决问题的能力,函数f(x)在区间(-1,1)不单调,转化为函数f'(x)在(-1,1)上存在零点是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
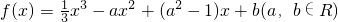
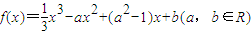

 的图象上横坐标为
的图象上横坐标为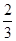 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数