Question

(1)求函数y＝x²－4x＋3的零点．

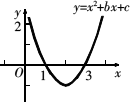
(2)已知二次函数y＝x²＋bx＋c的图象与x轴相交于(1，0)与(3，0)两点，求不等式x²＋bx＋c＞0的解集．

(3)若不等式x²＋bx＋c＞0的解集为{x|x＞3，或x＜1}，求实数b，c的值．

Answer 1

答案：
解析：

(1)分析：函数y＝f(x)的零点即为方程f(x)＝0的实数根，也就是函数y＝f(x)的图象与x轴交点的横坐标． 　　解：令y＝0，有x2－4x＋3＝0，解得x1＝1，x2＝3， 　　所以函数y＝x2－4x＋3的零点为1，3． 　　(2)分析：如图，二次函数y＝x2＋bx＋c的图象开口向上且与x轴有两个交点，则不等式x2＋bx＋c＞0的解集是使得y＝x2＋bx＋c图象上的点在x轴上方的x的取值范围． 　　解：不等式x2＋bx＋c＞0的解集为{x|x＞3，或x＜1}． 　　(3)分析：由(1)知，方程ax2＋bx＋c＝0的实数解函数y＝ax2＋bx＋c的图象上的点(x，0)中的x；由(2)知，不等式ax2＋bx＋c＞0(a＞0)的解集函数y＝ax2＋bx＋c(a＞0)图象上的点在x轴上方的x的取值范围．所以由不等式x2＋bx＋c＞0的解集为{x|x＞3，或x＜1}知，方程x2＋bx＋c＝0的两个根分别为x1＝1，x2＝3． 　　解：由题意知，方程x2＋bx＋c＝0的两个根分别为x1＝1，x2＝3． 利用根与系数的关系，有x1＋x2＝－b＝1＋3＝4，x1x2＝c＝1×3＝3，所以b＝－4，c＝3．