题目内容
求函数y=x2-2ax-1在[0,2]上的最值.
解:由已知得y=(x-a)2-1-a2,
(1)当a<0时,[0,2]是函数的递增区间,见图(1).
故函数在x=0时,取得最小值-1,在x=2时取得最大值3-4a.
(2)当0≤a≤1时,结合函数图象(见图(2))知,
函数在x=a时取得最小值-a2-1.
在x=2 时取得最大值3-4a.
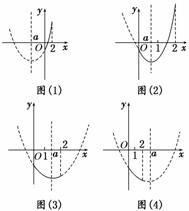
(3)当1<a≤2时,结合图象(见图(3))知,
函数在x=a时取得最小值-a2-1,
在x=0时取得最大值-1.
(4)当a>2时,[0,2]是函数的递减区间,见图(4).
函数在x=0时取得最大值-1,
在x=2时取得最小值3-4a.
综合上述ymax=![]()
ymin=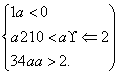

练习册系列答案
相关题目
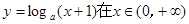 内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围