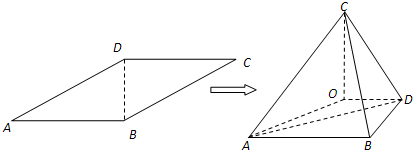
题目内容
如图,平行四边形ABCD中,AB⊥BD,AB=2,BD=
,沿BD将△BCD折起,使二面角A-BD-C为锐二面角,设C在平面ABD上的射影为O,若AD⊥BC
(1)求二面角A-BD-C的大小.
(2)求AC与平面COD所成角的正切值
(3)在线段BC上是否存在一点P,使得PD∥面AOC,若存在,求出P点位置并证明;若不存在,请说明理由
| 2 |
(1)求二面角A-BD-C的大小.
(2)求AC与平面COD所成角的正切值
(3)在线段BC上是否存在一点P,使得PD∥面AOC,若存在,求出P点位置并证明;若不存在,请说明理由

分析:(1)利用三垂线定定理和 BD⊥CD,OC⊥平面ODBA,可得BD⊥OD.即可得出∠CDO即为二面角A-BD-C的平面角.连接OB,利用CO⊥平面ABD,AD⊥BC,可得AD⊥OB,进而得到∠OBD=∠DAB,于是Rt△ABD∽Rt△BDO,利用其性质可得OD=1,在Rt△COD中,利用边角关系即可得出∠CDO.
(2)利用CO⊥面ABD,可得面COD⊥面ABD.过A作AM⊥DO交DO延长线于M点,连CM,则AM⊥面COD.即可得出∠ACM即为AC与平面COD所成角.
在△CMD中,利用等腰三角形的性质可得CM.AM=BD=
.即可得出
(3)取BC的中点P,AC的中点E,连接PD,PE,OE.利用三角形的中位线定理、平行四边形的判定与性质定理、线面平行的判定定理即可得出.
(2)利用CO⊥面ABD,可得面COD⊥面ABD.过A作AM⊥DO交DO延长线于M点,连CM,则AM⊥面COD.即可得出∠ACM即为AC与平面COD所成角.
在△CMD中,利用等腰三角形的性质可得CM.AM=BD=
| 2 |
(3)取BC的中点P,AC的中点E,连接PD,PE,OE.利用三角形的中位线定理、平行四边形的判定与性质定理、线面平行的判定定理即可得出.
解答:解:(1)∵BD⊥CD,OC⊥平面ODBA,∴BD⊥OD.
∴∠CDO即为二面角A-BD-C的平面角.
连接OB,∵CO⊥平面ABD,AD⊥BC,
∴AD⊥平面BOC,∴AD⊥OB,
∴∠OBD+∠ADB=90°,
故∠OBD=∠DAB,∴Rt△ABD∽Rt△BDO,
∴
=
,∴OD=
=
=1,
在Rt△COD中,cos∠CDO=
=
,得∠CDO=60°.
(2)∵CO⊥面ABD,∴面COD⊥面ABD.
过A作AM⊥DO交DO延长线于M点,连CM,则AM⊥面COD.
∴∠ACM即为AC与平面COD所成角.
在△CMD中,CO⊥DM,OM=OD=1,∴CM=CD=2.
又AM=BD=
∴tan∠ACM=
=
,即AC与平面COD所成角的正切值为
.
(3)取BC的中点P,AC的中点E,连接PD,PE,OE
∵PE是△ABC的中位线,∴PE∥AB,PE=
AB=1,又OD∥AB,OD=1
∴PE∥OD,PE=OD
∴四边形PEOD为平行四边形,∴PD∥OE,又OE?面AOC,PD?面AOC,
∴PD∥面AOC
即存在BC的中点P,满足PD∥面AOC
∴∠CDO即为二面角A-BD-C的平面角.
连接OB,∵CO⊥平面ABD,AD⊥BC,
∴AD⊥平面BOC,∴AD⊥OB,
∴∠OBD+∠ADB=90°,
故∠OBD=∠DAB,∴Rt△ABD∽Rt△BDO,
∴
| OD |
| BD |
| BD |
| AB |
| BD2 |
| AB |
(
| ||
| 2 |

在Rt△COD中,cos∠CDO=
| OD |
| CD |
| 1 |
| 2 |
(2)∵CO⊥面ABD,∴面COD⊥面ABD.
过A作AM⊥DO交DO延长线于M点,连CM,则AM⊥面COD.
∴∠ACM即为AC与平面COD所成角.
在△CMD中,CO⊥DM,OM=OD=1,∴CM=CD=2.
又AM=BD=
| 2 |
∴tan∠ACM=
| AM |
| CM |
| ||
| 2 |
| ||
| 2 |
(3)取BC的中点P,AC的中点E,连接PD,PE,OE
∵PE是△ABC的中位线,∴PE∥AB,PE=
| 1 |
| 2 |
∴PE∥OD,PE=OD
∴四边形PEOD为平行四边形,∴PD∥OE,又OE?面AOC,PD?面AOC,
∴PD∥面AOC
即存在BC的中点P,满足PD∥面AOC
点评:本题综合考查了线面平行与垂直的判定定理与性质定理、空间角、三垂线定理、三角形的中位线定理、平行四边形的判定与性质定理,考查了空间想象能力、计算能力和推理能力.

练习册系列答案
相关题目
 如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF=
如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF= 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD. 如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若
如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若 (2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则
(2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则 如图,平行四边形ABCD中,
如图,平行四边形ABCD中,