题目内容
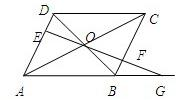如图，平行四边形ABCD的对角线交于点O，过点O的直线交AD于E，BC于F，交AB延长线于G，已知AB=a，BC=b，BG=c，则BF=分析：根据两条直线平行，得到三角形相似，根据相似三角形对应边成比例，得到一系列比例式，根据三角形全等，得到边长相等，利用等量代换变化出要求的量，根据方程思想，得到结果．
解答：解：∵BF∥AE
∴
=
=
=
，
∴
=
，
即BF=
．
故答案为：
∴
| BG |
| AG |
| BF |
| AE |
| BF |
| AD-BF |
| BF |
| BC-BF |
∴
| c |
| a+c |
| BF |
| c-BF |
即BF=
| bc |
| a+2c |
故答案为：
| bc |
| a+2c |
点评：本题考查三角形相似对应边成比例，考查等量代换思想，考查方程思想的应用，是一个比较典型的题目，本题是平面几何中常见的类型．
练习册系列答案
相关题目
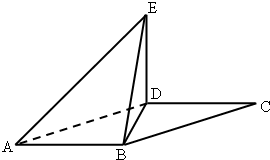如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
如图，平行四边形ABCD中，E，F分别是BC，DC的中点，G为交点，若
（2012•枣庄一模）如图，平行四边形ABCD中，点E是边BC（靠近点B）的三等分点，F是AB（靠近点A）的三等分点，P是AE与DF的交点，则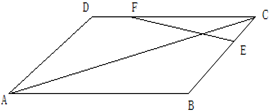
如图，平行四边形ABCD中，