题目内容
已知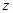 是复数,
是复数,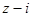 和
和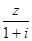 均为实数.
均为实数.
(1)求复数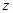 ;
;
(2)若复数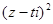 在复平面内对应点在第一象限,求实数t的取值范围.
在复平面内对应点在第一象限,求实数t的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由于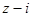 为实数,设为
为实数,设为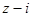
 ,故
,故 ,根据
,根据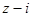 和
和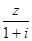 都是实数虚部都等于0,得到复数的代数形式,即可求出a,进而求出z.(II)根据上一问做出的复数的结果,代入复数
都是实数虚部都等于0,得到复数的代数形式,即可求出a,进而求出z.(II)根据上一问做出的复数的结果,代入复数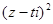 ,利用复数的加减和乘方运算,写出代数的标准形式,根据复数对应的点在第一象限,写出关于实部大于0和虚部大于0,解不等式组,得到结果.
,利用复数的加减和乘方运算,写出代数的标准形式,根据复数对应的点在第一象限,写出关于实部大于0和虚部大于0,解不等式组,得到结果.
解:(1)∵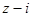 为实数,设为
为实数,设为 ,∴
,∴ (2分)
(2分)
∴ 为实数 ∴
为实数 ∴ (5分)
(5分)
∴ (6分)
(6分)
(2) (8分)
(8分)
∵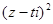 对应点在第一象限,
对应点在第一象限,
∴ (l0分) 解得:
(l0分) 解得: (12分)
(12分)
考点:复数代数形式的混合运算;复数的代数表示法及其几何意义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
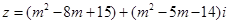 是(1)实数;(2)纯虚数.
是(1)实数;(2)纯虚数.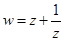 是实数,且
是实数,且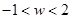 .
.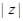 的值及z的实部的取值范围.
的值及z的实部的取值范围.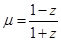 ,求
,求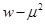 的最小值.
的最小值. .
. ,求
,求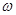 ;
; ,求实数
,求实数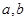 的值.
的值.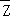 ﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.
﹣a﹣bi|﹣2|z|=0,求z为何值时,|z|有最小值,并求出|z|的值.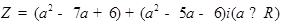 试求当a为何值时,Z为(1)实数,(2)虚数,(3)纯虚数。
试求当a为何值时,Z为(1)实数,(2)虚数,(3)纯虚数。 ,则复数
,则复数 在复平面上对应的点位于第 象限。
在复平面上对应的点位于第 象限。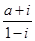 为纯虚数,则
为纯虚数,则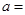 .
.