题目内容
设数列{an}、{bn}的各项都是正数,Sn为数列{an}的前n项和,且对任意n∈N*,都有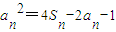 ,b1=e,
,b1=e,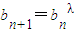 ,cn=an+1•lnbn(常数λ>0,lnbn是以为底数的自然对数,e=2.71828…)
,cn=an+1•lnbn(常数λ>0,lnbn是以为底数的自然对数,e=2.71828…)(1)求数列{an}、{bn}的通项公式;
(2)用反证法证明:当λ=4时,数列{cn}中的任何三项都不可能成等比数列;
(3)设数列{cn}的前n项和为Tn,试问:是否存在常数M,对一切n∈N*,(1-λ)Tn+λcn≥M恒成立?若存在,求出M的取值范围;若不存在,请证明你的结论.
【答案】分析:(1)由条件 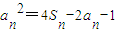 ①,求得a1=1.当n≥2时,有
①,求得a1=1.当n≥2时,有  ②,由①-②可得数列{an}是公差等于2的等差数列,从而求得an=2n-1.再由
②,由①-②可得数列{an}是公差等于2的等差数列,从而求得an=2n-1.再由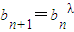 ,且bn>0,可得lnbn=lnb1×λn-1=λn-1,从而求得 bn=
,且bn>0,可得lnbn=lnb1×λn-1=λn-1,从而求得 bn=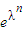 .
.
(2)当λ=4时,假设第m项、第n项、第k项成等比数列,则有 (2n+1)2•42n-2=(2m+1)4m-1•(2k+1)4k-1,即 m2+k2+mk+m+k=0,显然,这样的正整数m、k不存在,故数列{cn}中的任何三项都不可能成等比数列.
(3)用错位相减法求得(1-λ)Tn=3+2λ(1+λ+λ2+…+λn-2)-(2n+1)λn,①当λ=1时,求出M的取值范围.②当λ≠1时,再求出M的取值范围,综合可得结论.
解答:解:(1)∵因为an>0, ①,当n=1时,a12=4S1-2a1-1,解得a1=1.
①,当n=1时,a12=4S1-2a1-1,解得a1=1.
当n≥2时,有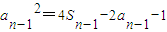 ②,
②,
由①-②得,(an+an-1)(an-an-1)=2(an+an-1),故有 an-an-1=2(n≥2),即数列{an}是公差等于2的等差数列,
所以an=a1+(n-1)d=1+(n-1)×2=2n-1.
又因为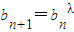 ,且bn>0,两边同时取自然对数得 lnbn+1=λlnbn,
,且bn>0,两边同时取自然对数得 lnbn+1=λlnbn,
由此可知数列{lnbn}是以lnb1=lne=1为首项,以λ为公比的等比数列,
所以lnbn=lnb1×λn-1=λn-1,所以,bn=eλn-1.
(2)当λ=4时,由(1)知,cn =an+1•lnbn =(2n+1)•λn-1=(2n+1)•4n-1.
假设第m项、第n项、第k项成等比数列,则有 (2n+1)2•42n-2=(2m+1)4m-1•(2k+1)4k-1,
即 (2n+1)2•42n-2=(2m+1)(2k+1)•4m+k-2,∴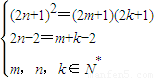 ,
,
∴(m+k+1)2=(2m+1)(2k+1),即 m2+k2+mk+m+k=0,显然,这样的正整数m、k不存在,故数列{cn}中的任何三项都不可能成等比数列.
(3)解:∵cn=an+1•lnbn =(2n+1)•λn-1,
∴Tn=3×λ0+5×λ1+7×λ2+…+(2n-1)×λn-2+(2n+1)×λn-1…③.
∴λ×Tn=3×λ1+5×λ2+7×λ3+…+(2n-1)×λn-1+(2n+1)×λn…④.
由③-④得-3Tn=3+2×4+2×42+…+2×4n-1-(2n+1)×4n=3+2×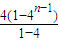 -(2n+1)4n=
-(2n+1)4n=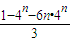 ,
,
所以,(1-λ)Tn=3+2λ(1+λ+λ2+…+λn-2)-(2n+1)λn.
①当λ=1时,(1-λ)Tn+λcn=(2n+1)(n∈N*)在N*上为单调递增函数,所以对于任意常数M∈(-∞,3],(1-λ)Tn+λcn=(2n+1)≥M恒成立.
②当λ≠1时,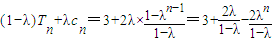 .
.
记g(n)=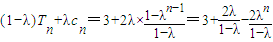 g(n+1)-g(n)=2λn>0,
g(n+1)-g(n)=2λn>0,
所以,数列g(n)为增函数.
所以当λ≠1时,g(n)=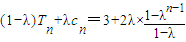 ≥g(1)=3.…(7分)
≥g(1)=3.…(7分)
所以,所以对于任意常数M∈(-∞,3],(1-λ)Tn+λcn≥M恒成立. …(8分)
点评:本题主要考查数列求和问题,用反证法和放缩法证明不等式,函数的恒成立问题,属于难题.
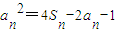 ①,求得a1=1.当n≥2时,有
①,求得a1=1.当n≥2时,有  ②,由①-②可得数列{an}是公差等于2的等差数列,从而求得an=2n-1.再由
②,由①-②可得数列{an}是公差等于2的等差数列,从而求得an=2n-1.再由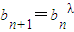 ,且bn>0,可得lnbn=lnb1×λn-1=λn-1,从而求得 bn=
,且bn>0,可得lnbn=lnb1×λn-1=λn-1,从而求得 bn=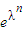 .
. (2)当λ=4时,假设第m项、第n项、第k项成等比数列,则有 (2n+1)2•42n-2=(2m+1)4m-1•(2k+1)4k-1,即 m2+k2+mk+m+k=0,显然,这样的正整数m、k不存在,故数列{cn}中的任何三项都不可能成等比数列.
(3)用错位相减法求得(1-λ)Tn=3+2λ(1+λ+λ2+…+λn-2)-(2n+1)λn,①当λ=1时,求出M的取值范围.②当λ≠1时,再求出M的取值范围,综合可得结论.
解答:解:(1)∵因为an>0,
 ①,当n=1时,a12=4S1-2a1-1,解得a1=1.
①,当n=1时,a12=4S1-2a1-1,解得a1=1.当n≥2时,有
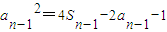 ②,
②,由①-②得,(an+an-1)(an-an-1)=2(an+an-1),故有 an-an-1=2(n≥2),即数列{an}是公差等于2的等差数列,
所以an=a1+(n-1)d=1+(n-1)×2=2n-1.
又因为
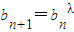 ,且bn>0,两边同时取自然对数得 lnbn+1=λlnbn,
,且bn>0,两边同时取自然对数得 lnbn+1=λlnbn,由此可知数列{lnbn}是以lnb1=lne=1为首项,以λ为公比的等比数列,
所以lnbn=lnb1×λn-1=λn-1,所以,bn=eλn-1.
(2)当λ=4时,由(1)知,cn =an+1•lnbn =(2n+1)•λn-1=(2n+1)•4n-1.
假设第m项、第n项、第k项成等比数列,则有 (2n+1)2•42n-2=(2m+1)4m-1•(2k+1)4k-1,
即 (2n+1)2•42n-2=(2m+1)(2k+1)•4m+k-2,∴
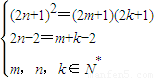 ,
,∴(m+k+1)2=(2m+1)(2k+1),即 m2+k2+mk+m+k=0,显然,这样的正整数m、k不存在,故数列{cn}中的任何三项都不可能成等比数列.
(3)解:∵cn=an+1•lnbn =(2n+1)•λn-1,
∴Tn=3×λ0+5×λ1+7×λ2+…+(2n-1)×λn-2+(2n+1)×λn-1…③.
∴λ×Tn=3×λ1+5×λ2+7×λ3+…+(2n-1)×λn-1+(2n+1)×λn…④.
由③-④得-3Tn=3+2×4+2×42+…+2×4n-1-(2n+1)×4n=3+2×
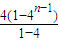 -(2n+1)4n=
-(2n+1)4n=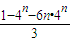 ,
,所以,(1-λ)Tn=3+2λ(1+λ+λ2+…+λn-2)-(2n+1)λn.
①当λ=1时,(1-λ)Tn+λcn=(2n+1)(n∈N*)在N*上为单调递增函数,所以对于任意常数M∈(-∞,3],(1-λ)Tn+λcn=(2n+1)≥M恒成立.
②当λ≠1时,
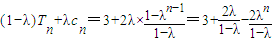 .
.记g(n)=
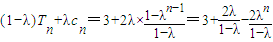 g(n+1)-g(n)=2λn>0,
g(n+1)-g(n)=2λn>0,所以,数列g(n)为增函数.
所以当λ≠1时,g(n)=
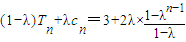 ≥g(1)=3.…(7分)
≥g(1)=3.…(7分)所以,所以对于任意常数M∈(-∞,3],(1-λ)Tn+λcn≥M恒成立. …(8分)
点评:本题主要考查数列求和问题,用反证法和放缩法证明不等式,函数的恒成立问题,属于难题.

练习册系列答案
相关题目