题目内容
用三段论推理命题:“任何实数的平方大于0,因为a是实数,所以a2>0”,你认为这个推理( )
| A.大前题错误 | B.小前题错误 | C.推理形式错误 | D.是正确的 |
A
解析试题分析:∵任何实数的平方大于0,因为a是实数,所以a2>0,
大前提:任何实数的平方大于0是不正确的,
故选A.
考点:演绎推理的基本方法.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
法国数学家费马观察到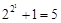 ,
, ,
, ,
, 都是质数,于是他提出猜想:任何形如
都是质数,于是他提出猜想:任何形如 N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数
N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数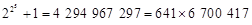 不是质数,从而推翻了费马猜想,这一案例说明( )
不是质数,从而推翻了费马猜想,这一案例说明( )
| A.归纳推理,结果一定不正确 | B.归纳推理,结果不一定正确 |
| C.类比推理,结果一定不正确 | D.类比推理,结果不一定正确 |
用反证法证明命题:“若整系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是
A.假设 都是偶数 都是偶数 |
B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个是偶数 至多有一个是偶数 |
D.假设 至多有两个是偶数 至多有两个是偶数 |
用反证法证明“自然数a,b,c中恰有一个偶数”时,下列假设正确的是 ( )
| A.假设a,b,c都是奇数或至少有两个偶数 |
| B.假设a,b,c都是偶数 |
| C.假设a,b,c至少有两个偶数 |
| D.假设a, b,c都是奇数 |
用数学归纳法证明1+2+3+…+n2= ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.k2+1 |
| B.(k+1)2 |
C. |
| D.(k2+1)+(k2+2)+…+(k+1)2 |
若P= +
+ ,Q=
,Q=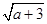 +
+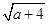 (a≥0),则P,Q的大小关系( )
(a≥0),则P,Q的大小关系( )
| A.P>Q | B.P=Q |
| C.P<Q | D.由a取值决定 |
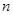 个图包含______个互不重叠的单位正方形。
个图包含______个互不重叠的单位正方形。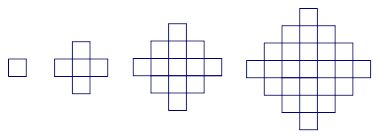

 =c+d
=c+d