题目内容
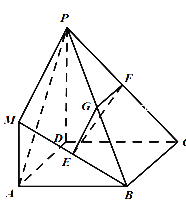
【题目】在如图所示的几何体中，四边形
是正方形， 
平面
, 
, 
、
、
分别为
、
、
的中点，且
.
（1）求证：平面
平面
；
（2）求证： 
平面
.
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）推导出
，由此证明面
面
（2）推导出
， 
，又
则可证得
平面
.
试题解析：
（1）证明：E，G,F分别为MB，PB，PC的中点，
，又四边形ABCD是正方形， 
在面PMA外，PM，AD在面PMA内， 
EG
面PMA，GF
面PMA，
又
都在平面EFG内且相交， 
面
面
（2）证明 由已知MA⊥平面ABCD，PD∥MA，
∴PD⊥平面ABCD.
又BC平面ABCD，∴PD⊥BC.
∵四边形ABCD为正方形，∴BC⊥DC.
又PD∩DC＝D，∴BC⊥平面PDC.
面
又
，在正方形
中， 
，
为
中点， 
，
又
,
平面
.
练习册系列答案
相关题目
