题目内容
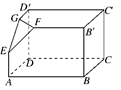
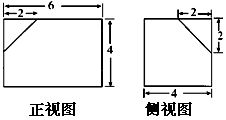
如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.试探究点M的位置,使F—AE—M为直二面角
.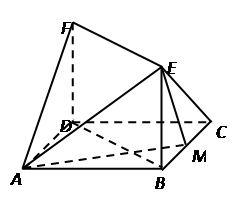
当M在BC的中点时, 平面AME⊥平面AEF。
解析试题分析:本小题适合采用空间向量法求解,以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,然后求出相关点的坐标,设M(λ,1,0),再设二面角F—AE—M的两个面的法向量,根据法向量垂直可得到关于λ的方程,从而求出λ的值,确定出点M的位置.
以D为坐标原点,分别以DA、DC、DF所在直线为x、y、z轴,建立空间直角坐标D-xyz,
依题意,得D(0,0,0),A(1,0,0),F(0,0,1),C(0,1,0),B(1,1,0),E(1,1,1),
设M(λ,1,0),平面AEF的法向量为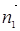 =(x1,y1,z1),平面AME的法向量为
=(x1,y1,z1),平面AME的法向量为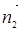 =(x2,y2,z2)
=(x2,y2,z2)
∵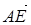 =(0,1,1),
=(0,1,1),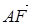 =(-1,0,1), ∴
=(-1,0,1), ∴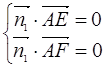 ∴
∴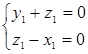
取z1=1,得x1=1,y1=-1 ∴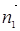 =(1,-1,0)
=(1,-1,0)
又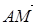 =(λ-1,1,0) ,
=(λ-1,1,0) ,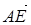 =(0,1,1),
=(0,1,1),
∴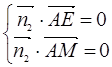 ∴
∴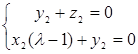
取x2=1得y2=1-λ,z2=λ-1 ∴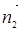 =(1,1-λ,λ-1)
=(1,1-λ,λ-1)
若平面AME⊥平面AEF,则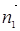 ⊥
⊥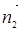 ∴
∴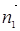
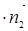 =0,
=0,
∴1-(1-λ)+(λ-1)=0,解得λ=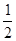 ,
,
此时M为BC的中点.
所以当M在BC的中点时, 平面AME⊥平面AEF. ……………12分.
考点:空间向量法研究二面角.
点评:利用空间向量法的优点是把几何证明转化为数值运算,解题的关键是建立一个恰当的坐标系,另外对相关点的坐标一定要认真仔细求对,否则会出现错误,问题无法进行.

练习册系列答案
相关题目
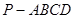 中,底面
中,底面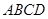 为平行四边形,
为平行四边形,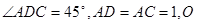 为
为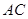 中点,
中点,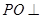 面
面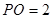 ,
, 为
为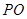 中点。
中点。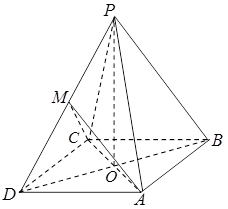
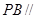 面
面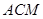 。
。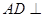 面
面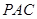 。
。 与平面
与平面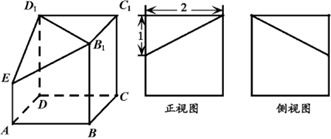
 垂直于⊙
垂直于⊙ 所在的平面,
所在的平面,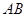 是⊙
是⊙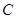 是⊙
是⊙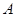 作
作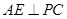 ,垂足为
,垂足为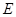 .
. 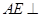 平面
平面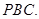

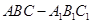 的各棱长均为2,侧面
的各棱长均为2,侧面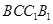
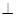 底面
底面 ,侧棱
,侧棱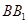 与底面
与底面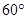 .
.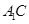 与底面
与底面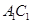 上是否存在点
上是否存在点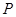 ,使得平面
,使得平面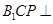 平面
平面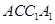 ?若存在,求出
?若存在,求出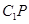 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。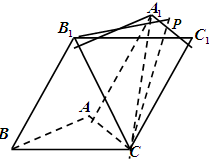
 中,
中,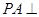 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱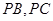 上,且
上,且
 平面
平面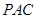 ;
; 的中点时,求
的中点时,求 与平面
与平面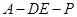 为直二面角?并说明理由.
为直二面角?并说明理由.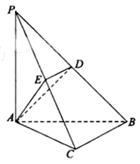
 的正方体
的正方体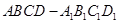 中,M,N分别是棱CD,AD的中点。(1)求证:四边形
中,M,N分别是棱CD,AD的中点。(1)求证:四边形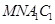 是梯形;(2)求证:
是梯形;(2)求证: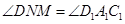


 ,直线PB与CD所成角为
,直线PB与CD所成角为 ,
,