题目内容
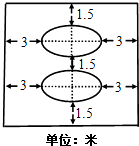
【题目】某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.
(注意:椭圆面积为πab,其中a,b分别为椭圆的长短半轴长)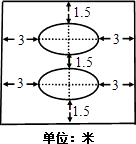
(1)根据图中所给数据,试用a、b表示S;
(2)当椭圆形花坛的长轴长为多少米时,所建矩形花园占地最少?并求出最小面积.
【答案】
(1)解:由题意得,S=(2a+6)(4b+ ![]() )=8ab+9a+24b+27
)=8ab+9a+24b+27
(2)解:∵πab=216π,∴ab=216
∴S=8ab+9a+24b+27≥8×216+27+2 ![]() =2187
=2187
当且仅当9a=24b,即a=24时,取“=”,此时2a=48
答:当椭圆形花坛的长轴为48米时,所建矩形花园占地最少,占地面积为2187平方米..…..
【解析】(1)根据图中所给数据,由题意得,S=(2a+6)(4b+ ![]() );(2)利用πab=216π,可得ab=216,再利用基本不等式即可得出结论.
);(2)利用πab=216π,可得ab=216,再利用基本不等式即可得出结论.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目