题目内容
已知由正数组成的数列{an}满足a1=1,a2=2,an2=an-1an+1(n≥2),则对数 的值为( )
的值为( )A.100
B.99
C.50
D.

【答案】分析:由正数组成的数列{an}满足a1=1,a2=2,an2=an-1an+1(n≥2),所以数列{an}是首项a1=1,公比q=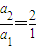 =2的等比数列,故a100=299,由此能求出
=2的等比数列,故a100=299,由此能求出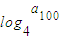 .
.
解答:解:∵由正数组成的数列{an}满足a1=1,a2=2,
an2=an-1an+1(n≥2),
∴数列{an}是首项a1=1,公比q=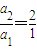 =2的等比数列,
=2的等比数列,
∴a100=299,
∴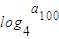 =log4299=
=log4299=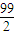 .
.
故选D.
点评:本题考查等比数列的性质和应用,是基础题.解题时要认真审题,注意数列的递推式的合理运用.
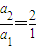 =2的等比数列,故a100=299,由此能求出
=2的等比数列,故a100=299,由此能求出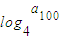 .
.解答:解:∵由正数组成的数列{an}满足a1=1,a2=2,
an2=an-1an+1(n≥2),
∴数列{an}是首项a1=1,公比q=
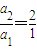 =2的等比数列,
=2的等比数列,∴a100=299,
∴
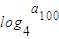 =log4299=
=log4299=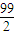 .
.故选D.
点评:本题考查等比数列的性质和应用,是基础题.解题时要认真审题,注意数列的递推式的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
 ,
,

 ,
,
