题目内容
(本小题共12分)已知由正数组成的数列{an}的前n项和为Sn= ,
,
①求S1,S2,S3;
②猜想Sn的表达式,并用数学归纳法证明你的结论;
③求
【答案】
①S1=1,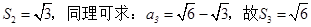
②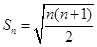 ,证明略
,证明略
③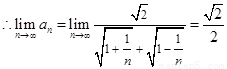
【解析】解:⑴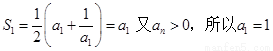 (1分)
(1分)
即S1=1, 又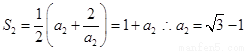
 (2分)
(2分)
故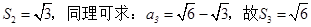 (3分)
(3分)
⑵猜想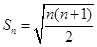 ,下面用数学归纳法证明:
(4分)
,下面用数学归纳法证明:
(4分)
①当n=1,2,3时,结论成立。
②假设当n=k(k≥3,k∈N*)时结论成立,则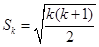 (6分)
(6分)
则当n=k+1时
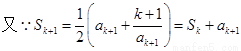
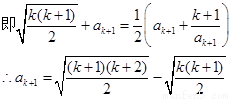
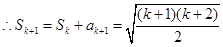
故当n=k+1时,结论成立。
综上①②得:对任意正整数n猜想均成立。 (9分)
③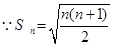 ,所以当n≥2时,
,所以当n≥2时,
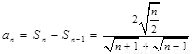
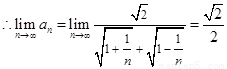 (12分)
(12分)

练习册系列答案
相关题目
 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间; 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( 与曲线
与曲线 为坐标原点),求直线
为坐标原点),求直线
 的最小正周期和最小值;
的最小正周期和最小值; ,
, ,求证:
,求证: .
.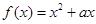 的最小值不小于
的最小值不小于 , 且
, 且 .
. 的解析式;
的解析式; 的最小值为实数
的最小值为实数 的函数
的函数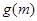 ,求函数
,求函数 ,集合
,集合
 ,求实数
,求实数 的取值范围.
的取值范围.