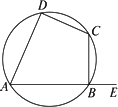
题目内容
已知：如图，四边形ABCD内接于⊙O，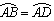
，过A点的切线交CB的延长线于E点，求证：AB2=BE·CD。
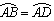，过A点的切线交CB的延长线于E点，求证：AB2=BE·CD。 
证明：连结AC，
因为EA切⊙O于A，
所以∠EAB=∠ACB，
因为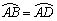
，
所以∠ACD=∠ACB，AB=AD，
于是∠EAB=∠ACD，
又四边形ABCD内接于⊙O，
所以∠ABE=∠D，
所以△ABE∽△CDA，
于是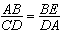
，即AB·DA=BE·CD，
所以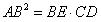
。
因为EA切⊙O于A，
所以∠EAB=∠ACB，
因为
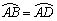，所以∠ACD=∠ACB，AB=AD，
于是∠EAB=∠ACD，
又四边形ABCD内接于⊙O，
所以∠ABE=∠D，
所以△ABE∽△CDA，
于是
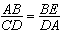，即AB·DA=BE·CD，所以
。
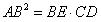练习册系列答案
星级口算天天练系列答案
相关题目
如图，四边形ABCD中，△BCD为正三角形，AD=AB=2，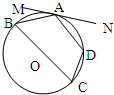
A．已知方程|2x-1|-|2x+1|=a+1有实数解，则a的取值范围为