题目内容
10.设x,y满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=abx+y(a>0,b>0)的最大值为5,则a+b的最小值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作可行域,平移目标直线可得直线过点(1,4)时,目标函数取最大值,可得ab=1,由基本不等式可得.
解答 解:作约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,所对应的可行域,(如图阴影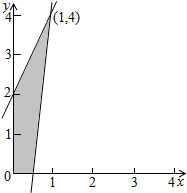
将z=abx+y变形为y=-abx+z,其中a>0,b>0,
4个顶点是(0,0),(0,2),($\frac{1}{2}$,0),(1,4),
由图易得目标函数在(1,4)取最大值5,
∴ab+4=5,即ab=1,
由基本不等式可得a+b≥2$\sqrt{ab}$=2,当且仅当a=b=1时取等号,
故选:B.
点评 本题考查线性规划,涉及基本不等式的应用,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.“A•B<0”是“方程Ax2+By2+Dx+Ey+C=0表示双曲线”的( )
| A. | 充分但非必要条件 | B. | 必要但非充分条件 | ||
| C. | 充要条件 | D. | 不充分也非必要条件 |
20.设函数f(x)是定义在R上的偶函数,且f(x+3)=-f(x),又当0<x≤1,f(x)=2x,则f(17.5)=( )
| A. | 1 | B. | -1 | C. | 11 | D. | -11 |