Question

已知函数f(x)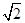＝sin.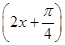

(1)求它的振幅、周期、初相；

(2)在所给坐标系中用五点法作出它在区间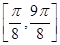上的图象.

(3)说明y＝sin x的图像可由y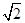＝sin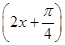的图像经过怎样的变换而得到．

 

Answer 1

【答案】

(1)y＝sin的振幅A＝，周期T＝＝π，初相φ＝.

（2）

（3）y＝sin x的图像可由y＝sin的图像，先将所有点的纵坐标缩短为原来的 倍，同时周期扩大为原来的2倍，同时向左平移个单位得到。

【解析】

试题分析：(1)y＝sin的振幅A＝，周期T＝＝π，初相φ＝.

列表：

2x＋	π	π	2π
x
f(x)＝sin	0	－	0

描点连线得图象如图：

(3)略.

考点：三角函数的图像与变换

点评：解决的关键是根据三角函数解析式来五点法作图，同时能结合三角函数的图像的变换来求解，属于基础题。