题目内容
(2012•汕头一模)已知向量
=(-2sin(π-x),cosx),
=(
cosx,2sin(
-x)),函数f(x)=1-
•
.
(1)求函数f(x)的解析式;
(2)当x∈[0,π]时,求f(x)的单调递增区间;
(3)说明f(x)的图象可以由g(x)=sinx的图象经过怎样的变换而得到.
| m |
| n |
| 3 |
| π |
| 2 |
| m |
| n |
(1)求函数f(x)的解析式;
(2)当x∈[0,π]时,求f(x)的单调递增区间;
(3)说明f(x)的图象可以由g(x)=sinx的图象经过怎样的变换而得到.
分析:(1)直接利用向量的数量积,通过二倍角公式与两角差的正弦函数,化简函数我一个角的一个三角函数的形式,即可求函数f(x)的解析式;
(2)利用正弦函数的单调增区间求出函数的单调增区间与x∈[0,π]取交集,即可求f(x)的单调递增区间;
法二通过x的范围,求出2x-
的范围,然后利用函数的最值时的2x-
的值,即可得到单调增区间.
(3)利用左加右减,与伸缩变换的原则,直接说明f(x)的图象可以由g(x)=sinx的图象经过变换而得到.
(2)利用正弦函数的单调增区间求出函数的单调增区间与x∈[0,π]取交集,即可求f(x)的单调递增区间;
法二通过x的范围,求出2x-
| π |
| 6 |
| π |
| 6 |
(3)利用左加右减,与伸缩变换的原则,直接说明f(x)的图象可以由g(x)=sinx的图象经过变换而得到.
解答:解:(1)∵
•
=-2sin(π-x)
cosx+2cosxsin(
-x)
=-2
sinxcosx+2cos2x=-
sin2x+cos2x+1 2分
∴f(x)=1-
•
=
sin2x-cos2x,…(3分)
∴f(x)=2sin(2x-
).…(4分)
(2)由-
+2kπ≤2x-
≤
+2kπ
,
解得-
+kπ≤x≤
+kπ
,…(6分)
∵取k=0和1且x∈[0,π],得0≤x≤
和
≤x≤π,
∴f(x)的单调递增区间为[0,
]和[
,π].…(8分)
法二:∵x∈[0,π],∴-
≤2x-
≤
,
∴由-
≤2x-
≤
和
≤2x-
≤
,…(6分)
解得0≤x≤
和
≤x≤π,
∴f(x)的单调递增区间为[0,
]和[
,π].…(8分)
(3)g(x)=sinx的图象可以经过下面三步变换得到f(x)=2sin(2x-
)的图象:g(x)=sinx的图象向右平移
个单位长度,再把所得各点的横坐标缩短到原来的
倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到f(x)=2sin(2x-
)的图象.…(14分)(每一步变换2分)
| m |
| n |
| 3 |
| π |
| 2 |
=-2
| 3 |
| 3 |
∴f(x)=1-
| m |
| n |
| 3 |
∴f(x)=2sin(2x-
| π |
| 6 |
(2)由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
|
解得-
| π |
| 6 |
| π |
| 3 |
|
∵取k=0和1且x∈[0,π],得0≤x≤
| π |
| 3 |
| 5π |
| 6 |
∴f(x)的单调递增区间为[0,
| π |
| 3 |
| 5π |
| 6 |
法二:∵x∈[0,π],∴-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
∴由-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 6 |
| 11π |
| 6 |
解得0≤x≤
| π |
| 3 |
| 5π |
| 6 |
∴f(x)的单调递增区间为[0,
| π |
| 3 |
| 5π |
| 6 |
(3)g(x)=sinx的图象可以经过下面三步变换得到f(x)=2sin(2x-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
点评:本题借助向量的数量积的化简,求解函数的解析式,考查三角函数的基本性质,函数的图象的变换.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
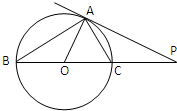 (2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为
(2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为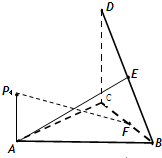 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.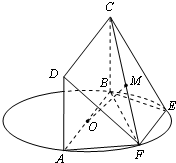 (2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.