题目内容
下列四个命题中：①
；②
；③设x，y都是正数，若
＝1，则x＋y的最小值是12；④若｜x－2｜＜
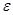，｜y－2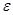｜＜，则｜x－y｜＜2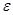，则其中所有真命题的个数有
| A．1个 | B．2个 | C．3个 | D．4个 |
A
解析试题分析：①只有当
，才成立，否则不成立；
②由基本不等式得
，当且仅当sin2x=2取等号，但是six2x=2无解，故不成立；③
，故③不成立，④由含绝对值不等式的性质可得：|x-y|=|（x-?）-（y-?）|≤|x-?|+ |y-?|＜?+ ? =2?，故④成立.所以选A.
考点：命题的真假判断与应用
点评：本题考查了基本不等式及含绝对值不等式性质的应用，熟练掌握以上知识（特别是等号成立的条件）是解决问题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知
，函数
，若
满足关于
的方程
，则下列选项的命题中为假命题的是（ ）
A． | B． |
C． | D． |
“
”是 “圆
经过原点”的
| A．充分而不必要条件 |
| B．必要而不充分条件 |
| C．充分必要条件 |
| D．既不充分也不必要条件 |
设p：log2x<0，q：
x－1>1，则p是q的 ( )．
| A．充要条件 | B．充分不必要条件 | C．必要不充分条件 | D．既不充分也不必要条件 |
下列有关命题的说法正确的是
A．命题“若 ，则 ”的否命题为：“若，则 ”． |
B．“ ”是“ ”的必要不充分条件． |
C．命题“ 使得 ”的否定是：“ 均有”． |
D．命题“若 ，则 ”的逆否命题为真命题． |
命题“对任意的
”的否定是
| A．不存在 | B．存在 |
C．存在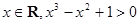 | D．对任意的 |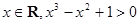
“
”是“
”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
若a，b都是实数，则“a－b＞0”是“a2－b2＞0”的 （）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
命题
对
，都有
成立，则
的否定形式为（ ）
A．对，都有 | B． ，都有 |
C．，都有 | D．对，都有 |