题目内容
若a,b都是实数,则“a-b>0”是“a2-b2>0”的 ()
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
D
解析试题分析:因为,a,b都是实数,所以,a-b>0时,无法确定a2-b2>0;
反之,当a2-b2>0时,因为无法确定得到a-b>0,故选D。
考点:充要条件的概念,不等式的性质。
点评:简单题,充要条件问题,往往综合性较强,需要综合应用所学知识加以处理。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
命题 ,则
,则 是
是
A.0 | B. |
C. | D. |
下列四个命题中:① ;②
;② ;③设x,y都是正数,若
;③设x,y都是正数,若 =1,则x+y的最小值是12;④若|x-2|<
=1,则x+y的最小值是12;④若|x-2|<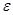 ,|y-2|<
,|y-2|<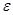 ,则|x-y|<2
,则|x-y|<2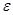 ,则其中所有真命题的个数有
,则其中所有真命题的个数有
| A.1个 | B.2个 | C.3个 | D.4个 |
设 ,则
,则 是
是 的 ( )
的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
条件 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是( )
| A.若f(x) 是偶函数,则f(-x)是偶函数 |
| B.若f(x)不是奇函数,则f(-x)不是奇函数 |
| C.若f(-x)是奇函数,则f(x)是奇函数 |
| D.若f(-x)不是奇函数,则f(x)不是奇函数 |
已知 是实数,则“
是实数,则“ 且
且 ”是“
”是“ 且
且 ”的( )条件
”的( )条件
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
已知命题 所有有理数都是实数,命题
所有有理数都是实数,命题 正数的对数都是负数,则下列命题中为真命题的是( )
正数的对数都是负数,则下列命题中为真命题的是( )
A. | B. | C. | D. |
命题“ ,都有
,都有 ”的否定是( )
”的否定是( )
A.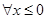 ,都有 ,都有 | B. ,都有 ,都有 |
C. ,使得 ,使得 | D. ,使得 ,使得 |