题目内容
设二元一次不等式组
所表示的平面区域为M,则过平面区域M的所有点中能使
取得最大值的点的坐标是
|
| y |
| x |
(1,9)
(1,9)
.分析:先根据约束条件画出可行域,设z=
,再利用z的几何意义求最值,只需求出过定点(0,0)直线过可行域内的点P时,斜率的值即可.
| y |
| x |
解答: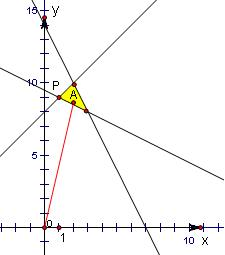 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,
设z=
,
将最大值转化为过定点O(0,0)的直线AO的斜率最大值,
由
得P(1,9).
当直线AO经过区域内的点P(1,9)时,z最大,
则过平面区域M的所有点中能使
取得最大值的点的坐标是 (1,9)
故答案为:(1,9).
 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,设z=
| y |
| x |
将最大值转化为过定点O(0,0)的直线AO的斜率最大值,
由
|
当直线AO经过区域内的点P(1,9)时,z最大,
则过平面区域M的所有点中能使
| y |
| x |
故答案为:(1,9).
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础.

练习册系列答案
相关题目
设二元一次不等式组
所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是( )
|
| A、[1,3] | ||
B、[2,
| ||
| C、[2,9] | ||
D、[
|
设二元一次不等式组
所表示的平面区域为M.若曲线x2-my2=1总经过区域M,则实数m的取值范围是( )
|
A、(-∞,
| ||
| B、[15,+∞) | ||
C、(
| ||
D、[
|