题目内容
设二元一次不等式组
所表示的平面区域为M.若曲线x2-my2=1总经过区域M,则实数m的取值范围是( )
|
A、(-∞,
| ||
| B、[15,+∞) | ||
C、(
| ||
D、[
|
分析:由于题目中给的曲线的方程中含有参数,故可选对参数m进行分类讨论,以确定曲线的方程,判断曲线的图象是椭圆、直线、圆还是双曲线,再根据对应曲线的性质,进行解答.
解答: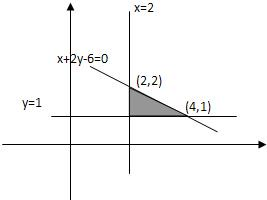 解:当m<0且m≠-1时,
解:当m<0且m≠-1时,
曲线为椭圆,则不经过区域M;
当m=-1时,
曲线为以原点为圆心,1为半径的圆,不经过区域M
当m=0时,x=±1,不经过区域M
当m>0时,
曲线为焦点在x轴上的双曲线,若总经过区域M,
则有4-4m=1解得m=
故离心率e12=
有16-m=1解得m=15故离心率e22=
根据双曲线的性质可得:e22≤e2≤e12
即有
≤1+
≤
所以
≤m≤15
故答案选D
 解:当m<0且m≠-1时,
解:当m<0且m≠-1时,曲线为椭圆,则不经过区域M;
当m=-1时,
曲线为以原点为圆心,1为半径的圆,不经过区域M
当m=0时,x=±1,不经过区域M
当m>0时,
曲线为焦点在x轴上的双曲线,若总经过区域M,
则有4-4m=1解得m=
| 3 |
| 4 |
| 7 |
| 3 |
有16-m=1解得m=15故离心率e22=
| 16 |
| 15 |
根据双曲线的性质可得:e22≤e2≤e12
即有
| 16 |
| 15 |
| 1 |
| m |
| 7 |
| 3 |
所以
| 3 |
| 4 |
故答案选D
点评:曲线mx2+ny2=1表示的图象形状受m,n取值的影响:①若m>n>0,则表示一条焦点在Y轴上的椭圆②若n>m>0,则表示一条焦点在X轴上的椭圆③若m=n>0,则表示一个圆④若m>0>n,则表示一条焦点在X轴上的双曲线⑤若n>0>m,则表示一条焦点在Y轴上的双曲线.

练习册系列答案
相关题目
设二元一次不等式组
所表示的平面区域为M,使函数y=ax(a>0,a≠1)的图象过区域M的a的取值范围是( )
|
| A、[1,3] | ||
B、[2,
| ||
| C、[2,9] | ||
D、[
|