��Ŀ����
���Ű����������ֺ�֮����ָ�Ӳ���������һ��������������Ⱥ����ʱ��ס������Ϊ�����壬��2.5�ף�ǰ��ǽ��2.5�ߵIJ�ɫ�ְ壬������2.5�ߵĸ��ϸְ壬���ְָ�ļ۸��ó��������㣨���ְ�ĸ߾�Ϊ2.5�ף��ó��ȳ��Ե��۾������ְ�ļ۸�ÿ���ۣ���ɫ�ְ�Ϊ450Ԫ�����ϸְ�Ϊ200Ԫ���������������Ͻ��죬ÿƽ���ײ��Ϸ�Ϊ200Ԫ��ÿ�����Ϸѿ�����32000Ԫ���ڡ�
��1���跿ǰ��ǽ�ij�Ϊ ������ǽ�ij�Ϊ
������ǽ�ij�Ϊ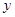 ��һ�������ò��Ϸ�Ϊp������
��һ�������ò��Ϸ�Ϊp������ ��
��
��2��һ�������S�����ֵ�Ƕ��٣���S���ʱ��ǰ��ǽ�ij����Ƕ��٣�
��1��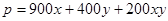
��2����S���ʱǰ��ǽ�ij����� ��
��
��������������⣺��1������ã����ݳ�����ı������ʽ��֪��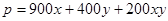
��2��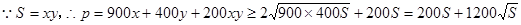
����Ϊ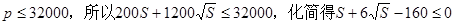 �����
�����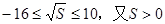 ,
, �����ҽ���
�����ҽ���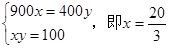 ʱSȡ��
ʱSȡ��
���ֵ����ÿ�������S�����ֵ��100ƽ���ף���S���ʱǰ��ǽ�ij����� �ס�
�ס�
���㣺��������ʽ
��������Ҫ�ǿ����˺���ģ�͵����ã���ϻ�������ʽ�����ֵ�������е��⡣

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
��֪����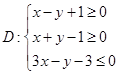 �����Ϊ
�����Ϊ ���㼯
���㼯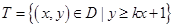 ������ϵ�ж�Ӧ��������Ϊ
������ϵ�ж�Ӧ��������Ϊ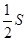 ����
���� ��ֵΪ�� ��
��ֵΪ�� ��
A�� | B�� | C�� | D�� |
�������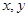 ��������
��������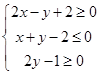 �ϣ���
�ϣ���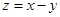 �����ֵ�� ��
�����ֵ�� ��
A�� | B��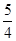 | C�� | D��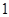 |

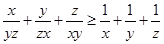 ��
�� ��9.
��9.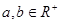 ����
����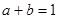 ����
����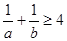 ��
��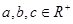 ����
����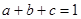 ����
����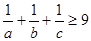 ��
��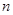 ������
������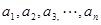 �Ľ��ۣ���д�����ۣ�����֤����
�Ľ��ۣ���д�����ۣ�����֤����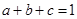 ����
����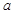 ��
�� ��
��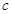 ����������֤��
����������֤��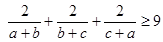 .
.