��Ŀ����
������D�ϵĺ�����������㣺���ڳ���M��0��������x��D����|f��x��|��M���������f��x����D�ϵ��н纯����
��1�����жϺ���f(x)=2sin(x+
)+3��ʵ����R�ϣ�����g(x)=x3+
��[
��3]���Dz����н纯�������ǣ������֤���������ǣ���˵�����ɣ�
��2������֪ij�ʵ���˶�����S��ʱ��t�Ĺ�ϵΪS(t)=
t4+3lnt-at��Ҫʹ��t��[
��3]��ÿһʱ�̵�˲ʱ�ٶȵľ���ֵ��������13����ʵ��a��ȡֵ��Χ��
��1�����жϺ���f(x)=2sin(x+
| �� |
| 6 |
| 3 |
| x |
| 1 |
| 3 |
��2������֪ij�ʵ���˶�����S��ʱ��t�Ĺ�ϵΪS(t)=
| 1 |
| 4 |
| 1 |
| 3 |
��1��������f(x)=2sin(x+
)+3��R�ϵ����ֵΪ5����СֵΪ-1��
���ڳ���M=5��������x��R����|f��x��|��M����f��x����R�����н纯����
��g(x)=x3+
��x��[1��3]����g/(x)=3x2-
��
��g/(x)=3x2-
=0����x=1��x=-1
����g��x����[
��1]�ϵ����ݼ���g��x����[1��3]�ϵ�����������g(3)��g(
)
��g��x����[
��3]�ϵ����ֵΪg��3��=28����СֵΪg��1��=4
���Դ��ڳ���M=28��������x��[
��3]����|g��x��|��M����g��x����[
��3]�����н纯����
��2����Ϊ�˶�����ΪS(t)=
t4+3lnt-at������˲ʱ�ٶ�V(t)=S/(t)=t3+
-a
�ɵ�t��[
��3]ʱ��|V��t��|��13���������|t3+
-a|��13��t��[
��3]�����
��
��t��[
��3]��������ɣ�1���ɵ�15��a��17
����ʵ��a��ȡֵ��Χ[15��17]
| �� |
| 6 |
���ڳ���M=5��������x��R����|f��x��|��M����f��x����R�����н纯����
��g(x)=x3+
| 3 |
| x |
| 3 |
| x2 |
��g/(x)=3x2-
| 3 |
| x2 |
����g��x����[
| 1 |
| 3 |
| 1 |
| 3 |
��g��x����[
| 1 |
| 3 |
���Դ��ڳ���M=28��������x��[
| 1 |
| 3 |
| 1 |
| 3 |
��2����Ϊ�˶�����ΪS(t)=
| 1 |
| 4 |
| 3 |
| t |
�ɵ�t��[
| 1 |
| 3 |
| 3 |
| t |
| 1 |
| 3 |
��
|
| 1 |
| 3 |
����ʵ��a��ȡֵ��Χ[15��17]

��ϰ��ϵ�д�
 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
�����Ŀ

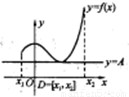
 ����ͼ��ʾ��������D�ϵĺ���f��x����������㣺��?x��D������A������f��x����A��������ƺ���f��x����D�����½磬����A��Ϊ�������½磮����ʾ��ͼ�еij���A������������Ҳ�����Ǹ������㣩
����ͼ��ʾ��������D�ϵĺ���f��x����������㣺��?x��D������A������f��x����A��������ƺ���f��x����D�����½磬����A��Ϊ�������½磮����ʾ��ͼ�еij���A������������Ҳ�����Ǹ������㣩
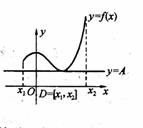 ����������12������ͼ��ʾ��������D�ϵĺ���
����������12������ͼ��ʾ��������D�ϵĺ���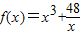 �ڣ�0��+�ޣ����Ƿ����½磿��˵�����ɣ�
�ڣ�0��+�ޣ����Ƿ����½磿��˵�����ɣ�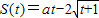 ��Ҫʹ��t��[0��+�ޣ��ϵ�ÿһʱ�̸��ʵ��˲ʱ�ٶ�����
��Ҫʹ��t��[0��+�ޣ��ϵ�ÿһʱ�̸��ʵ��˲ʱ�ٶ�����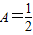 Ϊ�½�ĺ�������ʵ��a��ȡֵ��Χ��
Ϊ�½�ĺ�������ʵ��a��ȡֵ��Χ��