题目内容
在△ABC中,“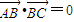 ”是“△ABC为直角三角形”的( )
”是“△ABC为直角三角形”的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
【答案】分析:先证明充分性,设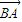 与
与 的夹角为α,利用平面向量的数量积运算法则化简
的夹角为α,利用平面向量的数量积运算法则化简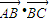 ,由已知
,由已知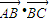 =0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.
=0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.
解答:解:当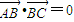 时,
时,
设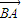 与
与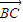 的夹角为α,
的夹角为α,
可得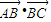 =ac•cos(π-α)=-ac•cosα,
=ac•cos(π-α)=-ac•cosα,
又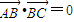 ,
,
∴-ac•cosα=0,即cosα=0,
∵α∈(0,π)
∴α=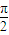 ,
,
则△ABC为直角三角形;
而当△ABC为直角三角形时,B不一定为直角,
故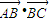 不一定等于0,
不一定等于0,
则在△ABC中,“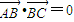 ”是“△ABC为直角三角形”的充分不必要条件.
”是“△ABC为直角三角形”的充分不必要条件.
故选A
点评:此题考查了充分,必要及充要条件的判断,三角形形状的判断,涉及的知识有:平面向量的数量积运算法则,余弦函数的奇偶性,以及特殊角的三角函数值,熟练掌握法则及余弦函数的奇偶性是解本题的关键.
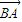 与
与 的夹角为α,利用平面向量的数量积运算法则化简
的夹角为α,利用平面向量的数量积运算法则化简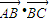 ,由已知
,由已知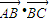 =0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.
=0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.解答:解:当
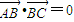 时,
时,设
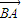 与
与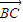 的夹角为α,
的夹角为α,可得
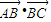 =ac•cos(π-α)=-ac•cosα,
=ac•cos(π-α)=-ac•cosα,又
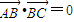 ,
,∴-ac•cosα=0,即cosα=0,
∵α∈(0,π)
∴α=
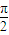 ,
,则△ABC为直角三角形;
而当△ABC为直角三角形时,B不一定为直角,
故
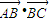 不一定等于0,
不一定等于0,则在△ABC中,“
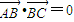 ”是“△ABC为直角三角形”的充分不必要条件.
”是“△ABC为直角三角形”的充分不必要条件.故选A
点评:此题考查了充分,必要及充要条件的判断,三角形形状的判断,涉及的知识有:平面向量的数量积运算法则,余弦函数的奇偶性,以及特殊角的三角函数值,熟练掌握法则及余弦函数的奇偶性是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,tanA是第3项为-4,第7项为4的等差数列的公差,tanB是第3项为,第6项为9的等比数列的公比,则△ABC是( )
| A、等腰三角形 | B、锐角三角形 | C、直角三角形 | D、钝角三角形 |
在△ABC中,CD是AB边上的高,a2+c2<b2,
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
A、A+B=
| ||
B、A-B=
| ||
C、B-A=
| ||
D、|A-B|=
|
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.