题目内容
在数列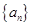 中,
中,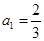 ,若函数
,若函数 ,在点
,在点 处切线过点
处切线过点
(1)求证:数列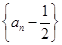 为等比数列;
为等比数列;
(2)求数列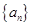 的通项公式和前n项和公式
的通项公式和前n项和公式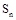 .
.
(1)详见解析;(2)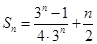 .
.
解析试题分析:(1)先求导函数 ,由导数的几何意义得
,由导数的几何意义得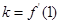 ,再求切线方程,将点
,再求切线方程,将点 代入得数列
代入得数列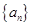 的递推式
的递推式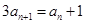 ,进而利用等比数列定义证明之;(2)求数列的前n项和,关键考察通项公式,根据通项公式的不同形式,选择相应的求和方法,一般情况下有①裂项相消法;②错位相减法;③分组求和法;④奇偶并项求和法,由(1)可得数列
,进而利用等比数列定义证明之;(2)求数列的前n项和,关键考察通项公式,根据通项公式的不同形式,选择相应的求和方法,一般情况下有①裂项相消法;②错位相减法;③分组求和法;④奇偶并项求和法,由(1)可得数列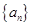 的通项公式
的通项公式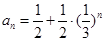 ,可利用分组求和法求和.
,可利用分组求和法求和.
试题解析:(1)因为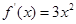 ,所以切线的斜率为
,所以切线的斜率为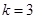 ,切点
,切点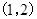 ,切线方程为
,切线方程为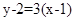 ,∴
,∴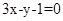 ,又因为过点
,又因为过点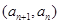 ,所以
,所以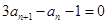 ,即
,即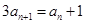 ①,
①,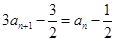 ,∴
,∴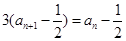 ,即
,即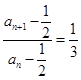 ,所以数列
,所以数列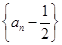 是等比数列,且公比
是等比数列,且公比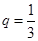 .
.
(2)由(1)得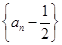 是公比为
是公比为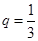 ,且首项为
,且首项为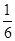 的等比数列,则
的等比数列,则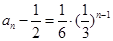 ,故
,故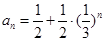 ,所以
,所以
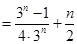 .
.
考点:1、导数的几何意义;2、等比数列定义;3、数列求和.

练习册系列答案
相关题目
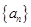 的前n项和记为
的前n项和记为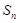 ,
,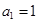 ,点
,点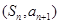 在直线
在直线 上,n∈N*.
上,n∈N*.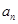 ;
;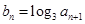 ,
,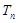 是数列
是数列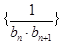 的前n项和,求
的前n项和,求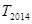 的值.
的值.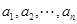 为
为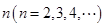 阶“期待数列”:
阶“期待数列”: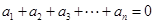 ;②
;②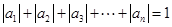 .
.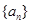 的通项公式是
的通项公式是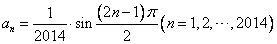 ,
, 为
为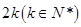 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 }的前n项和为
}的前n项和为 ,
,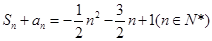 .
.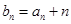 ,证明:数列
,证明:数列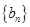 是等比数列;
是等比数列;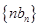 的前
的前 项和
项和 ;
;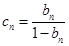 ,数列
,数列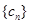 的前
的前
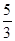 .
.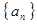 ,
,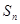 是其前
是其前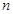 项的和,且满足
项的和,且满足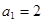 ,对一切
,对一切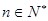 都有
都有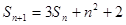 成立,设
成立,设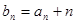 .
.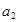 ;
;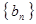 是等比数列;
是等比数列;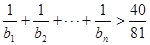 成立的最小正整数
成立的最小正整数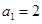 ,
,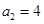 ,数列
,数列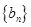 满足:
满足: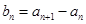 ,
,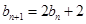 .
. 是等比数列(要指出首项与公比);
是等比数列(要指出首项与公比);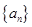 的通项公式.
的通项公式.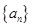 的前
的前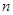 项和为
项和为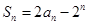 ,
,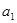 ,
,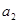 ;
;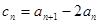 ,证明:数列
,证明:数列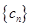 是等比数列;
是等比数列;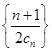 的前
的前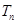 .
.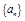 的前
的前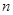 项和为
项和为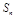 ,
,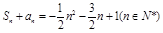 .
.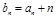 ,证明:数列
,证明:数列 是等比数列;
是等比数列;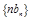 的前
的前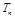 .
.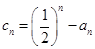 ,
,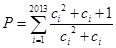 ,求不超过
,求不超过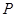 的最大的整数值.
的最大的整数值.