题目内容
 如图,已知OA=6,AB=3,AB⊥AO,∠xOA=θ,θ∈(0,
如图,已知OA=6,AB=3,AB⊥AO,∠xOA=θ,θ∈(0,| π | 2 |
(1)用θ表示点B的纵坐标y;
(2)求y的最大值.
分析:(1)分别过点A,B作x轴的垂线,过A作AE⊥BD与E,在三角形中.利用锐角三角函数的定义可求y
(2)由(1)的表,利用辅助角公式及三角函数的性质即可求解
(2)由(1)的表,利用辅助角公式及三角函数的性质即可求解
解答:解:(1)分别过点A,B作x轴的垂线,垂足分别为C,D,过A作AE⊥BD与E,
则∠ABE=∠xOA=θ,且有y=BE+ED=BE+AC=3cosθ+6sinθ,其中θ∈(0,
)…..(8分)
(2)由(1)知y=6sinθ+3cosθ=3
sin(θ+?),其中?为锐角且tan?=
故y有最大值为3
…..(14分)
则∠ABE=∠xOA=θ,且有y=BE+ED=BE+AC=3cosθ+6sinθ,其中θ∈(0,
| π |
| 2 |
(2)由(1)知y=6sinθ+3cosθ=3
| 5 |
| 1 |
| 2 |
故y有最大值为3
| 5 |
点评:本题主要考查了锐角三角函数的应用,辅助角公式在求解三角函数的最值中的应用,其中辅助角公式的应用是求解问题的关键

练习册系列答案
相关题目
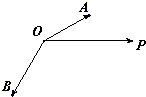 如图,已知单位向量
如图,已知单位向量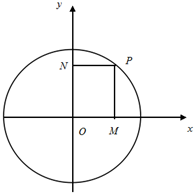 如图,已知P是单位圆(圆心在坐标原点)上一点,∠xOP=
如图,已知P是单位圆(圆心在坐标原点)上一点,∠xOP= 如图,已知
如图,已知