题目内容
1．在四边形ABCD中，P．Q分别是对角线AC．BD．的中点，E，G，F，H分别是边AD，AB，BC，CD的中点．求证：EF，GH，PQ的中点重合．分析 如图，连接EG，GF，FH，HE，EQ，QF，FP，EP，则由中位线定理即得结论．
解答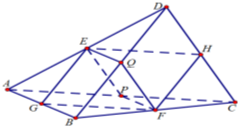 
证明：连接EG，GF，FH，HE，
由中位线定理有：
GE∥BD∥FH，GF∥AC∥EH，
所以EGFH是平行四边形，
所以EF，GH交点为其中点．
再连接EQ，QF，FP，EP，
同理EQFP也是平行四边形，
所以EF，QP交点为其中点，
所以三线共点，且交点为三线段的中点．
点评 本题考查平面图形的位置关系、中位线定理、三点共线问题，属中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
12．已知曲线y=x2+2x-1在点M处的切线与x轴平行，则点M的坐标是（ ）
| A． | （-2，2） | B． | （-2，-2） | C． | （-1，2） | D． | （-1，-2） |
9．如图，PA⊥面ABC，△ABC中BC⊥AC，则△PBC是（ ）
| A． | 直角三角形 | B． | 锐角三角形 | C． | 钝角三角形 | D． | 以上都有可能 |
10．若函数f（x）=$\frac{sinx}{x}$，并且$\frac{π}{3}$＜a＜b＜$\frac{2π}{3}$，则下列各结论中正确的是（ ）
| A． | f（a）＜f（$\sqrt{ab}$）＜f（$\frac{a+b}{2}$） | B． | f（$\sqrt{ab}$）＜f（$\frac{a+b}{2}$）＜f（b） | C． | f（$\sqrt{ab}$）＜f（$\frac{a+b}{2}$）＜f（a） | D． | f（b）＜f（$\frac{a+b}{2}$）＜f（$\sqrt{ab}$） |