如图.PA⊥面ABC.△ABC中BC⊥AC.则△PBC是( )A．直角三角形B．锐角三角形C．钝角三角形D．以上都有可能题目和参考答案——青夏教育精英家教网—

题目内容

9．如图，PA⊥面ABC，△ABC中BC⊥AC，则△PBC是（　　）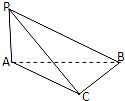

A．

直角三角形

B．

锐角三角形

C．

钝角三角形

D．

以上都有可能

分析由已知PA⊥面ABC，利用线面垂直的性质定理得到PA⊥BC，结合BC⊥AC，利用线面垂直的判定定理得到BC⊥平面PAC，再次利用线面垂直的性质定理得到BC⊥PC，从而判断△PBC的形状．

解答解：∵PA⊥面ABC，BC?平面ABC
∴PA⊥BC
又△ABC中BC⊥AC，
∴BC⊥平面PAC
∴BC⊥PC；
即△PBC是直角三角形．
故选：A．

点评本题考查了线面垂直的判定定理和性质定理的运用；体现了线面关系与线线关系的转化．

练习册系列答案

相关题目

19．

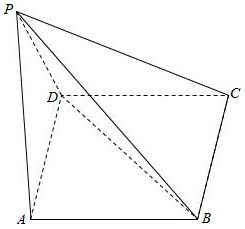如图，四凌锥P-ABCD而底面ABCD是矩形，侧面PAD是等腰直角三角形∠APD=90°，且平面PAD⊥平面ABCD．
（Ⅰ）求证：PA⊥PC；
（Ⅱ）在AD=2，AB=4，求三棱锥P-ABD的体积；
（Ⅲ）在条件（Ⅱ）下，求四棱锥P-ABCD外接球的表面积．

20．

如图，将边长为1的正方形ABCD，沿对角线BD折起来，使平面ABD⊥平面C′BD，则AC′=（　　）

17．设集合P={x|x=a+b$\sqrt{3}$，a、b∈N}，对于其中任意两个元素进行加法、减法、除法（除数不能为零）的运算，其结果是否仍属于集合P，证明你的结论．

4．已知sin（$\frac{π}{2}$+α）=-$\frac{4}{5}$，α$∈（π，\frac{3π}{2}）$，求cos（$\frac{π}{3}-α$）的值．

14．已知函数f（x）=（x²-3x+3）•e^x定义域为[-2，t]（t＞-2）．
（1）试确定t的取值范围，使得函数f（x）在[-2，t]上为单调函数；
（2）证明：对于任意的t＞-2，总存在x₀∈（-2，t），满足$\frac{{f'（{x_0}）}}{{{e^{x_0}}}}$=$\frac{2}{3}$（t-1）²，并确定这样的x₀的个数．

1．在四边形ABCD中，P．Q分别是对角线AC．BD．的中点，E，G，F，H分别是边AD，AB，BC，CD的中点．求证：EF，GH，PQ的中点重合．

18．tan$\frac{π}{8}$-$\frac{1}{tan\frac{π}{8}}$的值是（　　）

19．求函数f（x）=e^x．（x≤1）的切线与坐标轴围城的三角形面积的最大值．

试题分类