题目内容
18.已知向量$\overrightarrow{m}$=(2sin$\frac{x}{2}$,-$\sqrt{3}$),$\overrightarrow{n}$=(1-2sin2$\frac{x}{4}$,cosx),(其中x∈R).(1)若$\overrightarrow{m}$⊥$\overrightarrow{n}$,求x的取值的集合;
(2)若f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-2t,当x∈[0,π]是函数f(x)有两个零点,求实数t的取值范围.
分析 (1)利用两个向量垂直的性质,可得sin(x-$\frac{π}{3}$)=0,从而求得x的取值的集合.
(2)由平面向量数量积的运算求得f(x),根据自变量的范围,确定函数的零点,即求f(x)=0的根,进一步求出实数t的取值范围.
解答 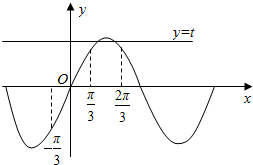 解:(1)∵$\overrightarrow{m}$⊥$\overrightarrow{n}$,
解:(1)∵$\overrightarrow{m}$⊥$\overrightarrow{n}$,
∴$\overrightarrow{m}$•$\overrightarrow{n}$=0,
∴2sin$\frac{x}{2}$(1-2sin2$\frac{x}{4}$)-$\sqrt{3}$cosx=0,
⇒sinx-$\sqrt{3}$cosx=0,
⇒sin(x-$\frac{π}{3}$)=0,
∴解得:x=kπ+$\frac{π}{3}$,k∈Z.
(2)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-2t=2sin$\frac{x}{2}$(1-2sin2$\frac{x}{4}$)-$\sqrt{3}$cosx-2t
=2sin(x-$\frac{π}{3}$)-2t,
∵在x∈[0,π]时,函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-2t有两个零点
∴f(x)=0有两个实数根,即函数图象有两个交点.
∴sin(x-$\frac{π}{3}$)=t在[0,π]上有两个根,
∵x∈[0,π],
∴x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
∴t∈[$\frac{\sqrt{3}}{2}$,1).
点评 本题重点考查知识点:三角函数的解析式的求法,以及在某一定义域下利用函数的零点求参数的取值范围问题.是很好的高考题型,属于中档题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 全集为1,A、B、C均为1的子集,则阴影部分表示的集合是(∁I(A∪C))∩B.
全集为1,A、B、C均为1的子集,则阴影部分表示的集合是(∁I(A∪C))∩B.