题目内容

已知函数f(x)=
1，x≤0
1
x
，x＞0
，则使方程x+f（x）=m有解的实数m的取值范围是（　　）
A、（1，2）
B、（-∞，-2）
C、（-∞，1）∪（2，+∞）
D、（-∞，1]∪[2，+∞）
分析：要使方程x+f（x）=m有解，即函数f(x)=
1，x≤0
1
x
，x＞0
与y=m-x的图象有交点，在同一坐标系中画出它们的图象，根据图象即可求得实数m的取值范围．
解答：解：方程x+f（x）=m有解，即方程f（x）=m-x有解，
在同一坐标系中画出f(x)=
1，x≤0
1
x
，x＞0
和y=m-x的图象，
根据图象，当x≤0时，m≤1，
当x＞0时，m=x+
1
x
≥2，当且仅当x=1时，等号成立，
综上，m≤1，或m≥2
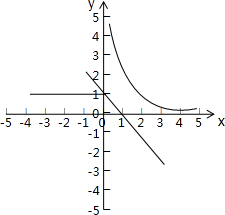
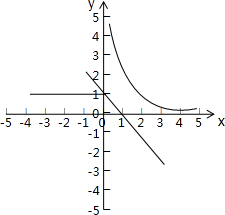
故选D．精英家教网
点评：此题是中档题．考查函数的零点与方程根 的关系，体现了转化和数形结合的思想，同时考查了学生分析解决问题的能力和计算能力．
练习册系列答案
相关题目
（1）、已知函数f(x)=
1+
2
cos(2x-
π
4
)
sin(x+
π
2
)
．若角α在第一象限且cosα=
3
5
，求f(α)．
（2）函数f(x)=2cos2x-2
3
sinxcosx的图象按向量
m
=(
π
6
，-1)平移后，得到一个函数g（x）的图象，求g（x）的解析式．
已知函数f(x)=(1-
a
x
)ex，若同时满足条件：
①?x0∈（0，+∞），x0为f（x）的一个极大值点；
②?x∈（8，+∞），f（x）＞0．
则实数a的取值范围是（　　）
已知函数f(x)=
1+lnx
x
．
（1）如果a＞0，函数在区间(a，a+
1
2
)上存在极值，求实数a的取值范围；
（2）当x≥1时，不等式f(x)≥
k
x+1
恒成立，求实数k的取值范围．
已知函数f(x)=
1+
1
x
，(x＞1)
x2+1，(-1≤x≤1)
2x+3，(x＜-1)
．
（1）求f(
1
2
-1
)与f（f（1））的值；
（2）若f(a)=
3
2
，求a的值．
定义在D上的函数f（x）如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数f(x)=
1-m•2x1+m•2x
．
（1）m=1时，求函数f（x）在（-∞，0）上的值域，并判断f（x）在（-∞，0）上是否为有界函数，请说明理由；
（2）若函数f（x）在[0，1]上是以3为上界的有界函数，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网