题目内容
7.已知,在△ABC中,∠C=90°,BC=6,AC=8,点M、N在△ABC的边上,将△ABC沿直线MN对折后,它的一个顶点正好落在对边上,且折痕MN截△ABC所成的小三角形(即对折后的重叠部分)与△ABC相似.请在下列图(不一定都用,不够可添)中分别画出折痕MN各种可能的位置,并说明画法及直接写出折痕的长.
分析 由已知条件利用三角形中位线性质、直角三角形相似的性质及垂直平公线性质及三角形相似的判定定理,能求出结果.
解答 (本小题满分12分)
解:∵在△ABC中,∠C=90°,BC=6,AC=8,点M、N在△ABC的边上,将△ABC沿直线MN对折后,
它的一个顶点正好落在对边上,且折痕MN截△ABC所成的小三角形(即对折后的重叠部分)与△ABC相似,
∴前3图分别为△ABC的中位线,长度分别是3、4、5…(6分)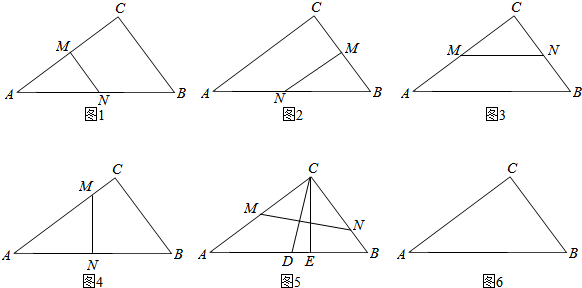
图4中N为AB的中点,MN垂直平分AB,MN=$\frac{15}{4}$,…(8分)
图5中D为AB的中点,MN垂直平分CD,MN=$\frac{125}{24}$.…(12分)
点评 本题考查使折痕MN截大三角形所成的小三角形(即对折后的重叠部分)与大三角相似的折痕位置的确定及折痕长度的求法,是中档题,解题时要认真审题,注意三角形相似的判定定理的合理运用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
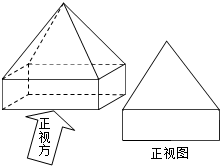
17.如图所示的一个几何体及其正视图如图,则其俯视图是( )

| A. |  | B. | 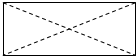 | C. | 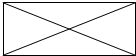 | D. |  |