题目内容
【题目】过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线
的直线交抛物线![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)经过坐标原点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,与抛物线
两点,与抛物线![]() 交于
交于![]() 点(
点(![]() ),若
),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)(方法一)依题意,设直线![]() 的方程为
的方程为![]() ,联立抛物线,然后再根据韦达定理,中点坐标公式求出
,联立抛物线,然后再根据韦达定理,中点坐标公式求出![]() 点坐标,消去参数
点坐标,消去参数![]() 得,即可求出动点
得,即可求出动点![]() 的轨迹方程.
的轨迹方程.
(方法二)利用点差法即可求出动点![]() 的轨迹方程.
的轨迹方程.
(2)直线![]() 的方程为
的方程为![]() ,方程联立后化为关于
,方程联立后化为关于![]() 的一元二次方程,写出根与系数关系,由弦长公式以及
的一元二次方程,写出根与系数关系,由弦长公式以及![]() 列出关系式,即可求出结果.
列出关系式,即可求出结果.
(1)依题意,![]() ,设直线
,设直线![]() 的方程为
的方程为![]()
由![]() 得
得![]() ,即
,即![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]()
消去参数![]() 得,动点
得,动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(方法二)设![]() ,
,![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
依题意,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
当![]() 时,
时,![]() 的中点为
的中点为![]() 也满足上式,
也满足上式,
所以,动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]()
由![]() ,得
,得![]() ,
,![]() 或
或![]() ,即
,即![]()
由![]() ,得
,得![]() ,
,![]()
设![]() ,则
,则![]() ,
,![]() ,
,![]()
![]()
由![]() ,得
,得![]() ,
,
解得![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度![]() (米)随着时刻
(米)随着时刻![]() 而周期性变化.为了了解变化规律,该团队观察若干天后,得到每天各时刻
而周期性变化.为了了解变化规律,该团队观察若干天后,得到每天各时刻![]() 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.6 | 1.0 |
(1)从![]() 中选择一个合适的函数模型,并求出函数解析式;
中选择一个合适的函数模型,并求出函数解析式;
(2)如果确定当浪高不低于0.8米时才进行训练,试安排白天内恰当的训练时间段.
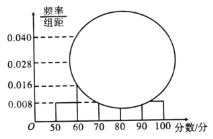
【题目】2019年某地遭遇严重干旱,某乡计划向上级申请支援,为上报需水量,乡长事先抽样调查100户村民的月均用水量,得到这100户村民月均用水量(单位:t)的频率分布表如下:
月均用水量分组 | 频数 | 频率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合计 | 100 | 1.00 |
(1)请完成该频率分布表,并画出相对应的频率分布直方图.
(2)样本的中位数是多少?
(3)已知上级将按每户月均用水量向该乡调水,若该乡共有1200户,请估计上级支援该乡的月调水量是多少吨.