题目内容
已知点M（-2，0）、N（2，0），动点P满足条件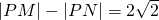
，则动点P的轨迹方程为
- A.x2-y2=2
- B.x2-y2=2（
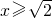） - C.x2-y2=2（
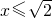） - D.y2-x2=2
B
分析：由已知中点M（-2，0），N（2，0），动点P满足条件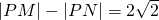．根据双曲线的定义，可得点P的轨迹是以M，N为焦点的双曲线的右支，进而得到答案．
解答：依题意，点P的轨迹是以M，N为焦点的双曲线的右支，
又∵M（-2，0），N（2，0），．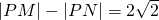
∴c=2，a=
∴所求方程为：
-
=1 （x
），
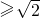即x2-y2=2（）．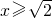
故选B．
点评：本题考查利用定义法求轨迹方程，若动点轨迹的条件符合某一基本轨迹的定义（如椭圆、双曲线、抛物线、圆等），可用定义直接探求．
分析：由已知中点M（-2，0），N（2，0），动点P满足条件
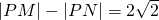．根据双曲线的定义，可得点P的轨迹是以M，N为焦点的双曲线的右支，进而得到答案．解答：依题意，点P的轨迹是以M，N为焦点的双曲线的右支，
又∵M（-2，0），N（2，0），
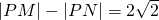．∴c=2，a=
∴所求方程为：
-=1 （x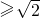），即x2-y2=2（
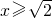）．故选B．
点评：本题考查利用定义法求轨迹方程，若动点轨迹的条件符合某一基本轨迹的定义（如椭圆、双曲线、抛物线、圆等），可用定义直接探求．
练习册系列答案
相关题目
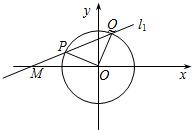已知点M（-2，0），⊙O：x2+y2=1（如图）；若过点M的直线l1交圆于P、Q两点，且圆孤PQ恰为圆周的