题目内容
下列命题中:
①若p、q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为:?x∈R,x2+2x+2≤0,则¬p为:?x∈R,x2+2x+2>0;
③若椭圆
+
=1的两焦点为F1,F2,且弦AB过F1点,则△ABF2的周长为20;
④若a、b、c是常数,则“a>0且b2-4ac<0”是“对任意x∈R,有ax2+bx+c>0”的充要条件.
在上述命题中,正确命题的序号是
①若p、q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为:?x∈R,x2+2x+2≤0,则¬p为:?x∈R,x2+2x+2>0;
③若椭圆
| x2 |
| 16 |
| y2 |
| 2 |
④若a、b、c是常数,则“a>0且b2-4ac<0”是“对任意x∈R,有ax2+bx+c>0”的充要条件.
在上述命题中,正确命题的序号是
②
②
.分析:①利用充分条件和必要条件的定义进行判断.②利用含有量词的命题的否定判断.③利用椭圆的定义进行判断.④利用充分条件和必要条件的定义进行判断.
解答:解:①若“p且q为真”,则p,q同时为真,若“p或q为真”,则p,q至少有一个位真,∴“p且q为真”是“p或q为真”的充分不必要条件,∴①错误.
②根据含有量词的命题的否定可知:¬p为:?x∈R,x2+2x+2>0,∴②正确.
③由椭圆的方程可知a=4,∵弦AB过F1点,∴△ABF2的周长为4a=16,∴③错误.
④若“a>0且b2-4ac<0”时,ax2+bx+c>0成立.当a=b=0,c>0时,不等式ax2+bx+c>0成立,但a>0且b2-4ac<0不成立,∴④错误.
故答案为:②.
②根据含有量词的命题的否定可知:¬p为:?x∈R,x2+2x+2>0,∴②正确.
③由椭圆的方程可知a=4,∵弦AB过F1点,∴△ABF2的周长为4a=16,∴③错误.
④若“a>0且b2-4ac<0”时,ax2+bx+c>0成立.当a=b=0,c>0时,不等式ax2+bx+c>0成立,但a>0且b2-4ac<0不成立,∴④错误.
故答案为:②.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
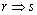 B.p:
B.p: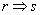 q:
q: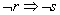
 q:
q:  D. p:
D. p: q:
q: