题目内容
(本小题满分12分)求证:32n+2-8n–9(n∈N*)能被64整除.
方法1:二项式定理
证明:32n+2-8n–9=9n+1-8n–9=(8+1)n+1-8n–9 ………………………………4分
=8n+1+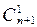 ·8n+…+
·8n+…+ ·82+
·82+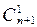 ·8+
·8+ -8n-9
-8n-9
=82(8n-1+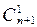 8n-2+…+
8n-2+…+ )+8(n+1)+1-8n-9…………………8分
)+8(n+1)+1-8n-9…………………8分
=64(8n-1+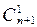 8n-2+…+
8n-2+…+ ) …………………………………10分
) …………………………………10分
∵8n-1+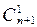 8n-2+…+
8n-2+…+ ∈Z,
∈Z,
∴32n+2-8n–9能被64整除. …………………………………12分
方法2:数学归纳法
(1)当n=1时,式子32n+2-8n–9=34-8-9=64能被64整除,命题成立.………………2分
(2)假设当n=k时,32k+2-8k-9能够被64整除. ………………………………4分
当n=k+1时,
32k+4-8(k+1)-9
=9[32k+2-8k-9]+64k+64
=9[32k+2-8k-9]+64(k+1) …………………………………8分
因为32k+2-8k-9能够被64整除,
∴9[32k+2-8k-9]+64(k+1)能够被64整除. …………………………………10分
即当n=k+1时,命题也成立.
由(1)(2)可知,32n+2-8n–9(n∈N*)能被64整除.……………………………12分
证明:32n+2-8n–9=9n+1-8n–9=(8+1)n+1-8n–9 ………………………………4分
=8n+1+
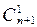 ·8n+…+
·8n+…+ ·82+
·82+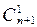 ·8+
·8+ -8n-9
-8n-9=82(8n-1+
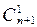 8n-2+…+
8n-2+…+ )+8(n+1)+1-8n-9…………………8分
)+8(n+1)+1-8n-9…………………8分=64(8n-1+
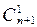 8n-2+…+
8n-2+…+ ) …………………………………10分
) …………………………………10分∵8n-1+
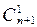 8n-2+…+
8n-2+…+ ∈Z,
∈Z,∴32n+2-8n–9能被64整除. …………………………………12分
方法2:数学归纳法
(1)当n=1时,式子32n+2-8n–9=34-8-9=64能被64整除,命题成立.………………2分
(2)假设当n=k时,32k+2-8k-9能够被64整除. ………………………………4分
当n=k+1时,
32k+4-8(k+1)-9
=9[32k+2-8k-9]+64k+64
=9[32k+2-8k-9]+64(k+1) …………………………………8分
因为32k+2-8k-9能够被64整除,
∴9[32k+2-8k-9]+64(k+1)能够被64整除. …………………………………10分
即当n=k+1时,命题也成立.
由(1)(2)可知,32n+2-8n–9(n∈N*)能被64整除.……………………………12分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则其解析式中
,则其解析式中 的系数为
的系数为  的二项
的二项 展开式中第五项的系数与第三项的系数的比是10:1.
展开式中第五项的系数与第三项的系数的比是10:1. 展开式中各项系数的和;
展开式中各项系数的和;
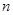 为奇数,
为奇数,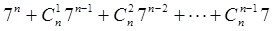 被
被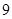 除所得的
除所得的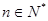 ,则1+
,则1+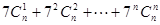 除以9的余数为 .
除以9的余数为 . ,则S等于
,则S等于

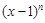

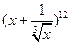 的展开式中的常数项是_____________.
的展开式中的常数项是_____________. 的展开式中,
的展开式中, 的系数为 .
的系数为 .