题目内容
函数 的定义域为 .
的定义域为 .
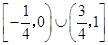
解析试题分析:由题意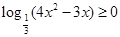 ,∴
,∴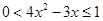 ,解得
,解得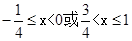 ,∴函数
,∴函数 的定义域为
的定义域为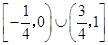
考点:本题考查了函数定义域的求法
点评:熟练掌握常见函数定义域的求法及对数不等式的解法是解决此类问题的关键,属基础题

练习册系列答案
相关题目
题目内容
函数 的定义域为 .
的定义域为 .
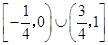
解析试题分析:由题意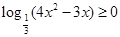 ,∴
,∴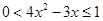 ,解得
,解得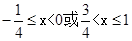 ,∴函数
,∴函数 的定义域为
的定义域为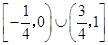
考点:本题考查了函数定义域的求法
点评:熟练掌握常见函数定义域的求法及对数不等式的解法是解决此类问题的关键,属基础题
