题目内容
已知定义在实数集R上的偶函数f(x)在区间[0,+∞)上是单调增函数.若f(1)<f(lnx),则x的取值范围是 .
(0, 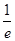 )∪(e, +∞)
)∪(e, +∞)
解析试题分析:解:①当lnx>0时,因为f(x)在区间[0,+∞)上是单调增函数
所以f(1)<f(lnx)等价于1<lnx,解之得x>e;②当lnx<0时,-lnx>0,结合函数f(x)是定义在R上的偶函数,可得f(1)<f(lnx)等价于f(1)<f(-lnx),再由函数f(x)在区间[0,+∞)上是单调增函数,得到1<-lnx,即lnx<-1,解之得0<x<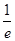
综上所述,得x的取值范围是x>e或0<x<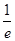 故答案为:(0,
故答案为:(0,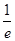 )∪(e,+∞).
)∪(e,+∞).
考点:函数的单调性
点评:本题在已知抽象函数的单调性和奇偶性的前提下,求解关于x的不等式,着重考查了函数的奇偶性与单调性等知识点,属于基础题.

练习册系列答案
相关题目
 的定义域为 .
的定义域为 . 的定义域为 .
的定义域为 . 的定义域为
的定义域为  =8,点
=8,点 在线段
在线段 =2,
=2, 为线段
为线段 上一动点,点
上一动点,点 绕点
绕点 绕点
绕点 .设
.设 =
= ,
, 
 的面积为
的面积为 .则
.则 的零点是 .
的零点是 . 
 的定义域是________________ .
的定义域是________________ . △
△ =
= ,其中
,其中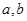 为正实数,若1△
为正实数,若1△ =3,则函数
=3,则函数 △
△ 的值域是 .
的值域是 . 是偶函数,且当
是偶函数,且当 时,
时, ,则当
,则当 时,
时, (
( >0)取最小值时相应的
>0)取最小值时相应的