题目内容
设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是( )
A.若直线AB与CD没有公共点,则AB∥CD
B.若AC与BD共面,则AD与BC共面
C.若AC与BD是异面直线,则AD与BC是异面直线
D.若AB=AC,DB=DC,则AD⊥BC
A
解析试题分析:空间两条直线有三种位置关系,有公共点的是相交,无没有公共点的可能平行也可能异面,故A错误,B中若AC与BD共面,则A、B、C、D四点共面,当然直线AD与BC也共面,B正确,由此C也正确(反证法),D中只要取BC中点O,连接AO,DO,易证直线BC⊥平面AOD,从而有AD⊥BC.
考点:两条直线的位置关系,空间点线共面问题.

练习册系列答案
相关题目
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )
| A.直线AB上 | B.直线BC上 | C.直线AC上 | D.△ABC内部 |
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.AB与SC所成的角等于DC与SA所成的角 |
| D.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
过直线 外两点作与直线
外两点作与直线 平行的平面,可以作( )
平行的平面,可以作( )
| A.1个 | B.1个或无数个 |
| C.0个或无数个 | D.0个、1个或无数个 |
给出下列命题
①过平面外一点有且仅有一个平面与已知平面垂直
②过直线外一点有且仅有一个平面与已知直线平行
③过直线外一点有且仅有一条直线与已知直线垂直
④过平面外一点有且仅有一条直线与已知平面垂直
其中正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
设 是两条不同直线,
是两条不同直线, 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( )
A. 且 且 则 则 | B. 且 且 ,则 ,则 |
C. 则 则 | D. 则 则 |
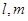 ,平面
,平面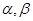 ,且
,且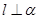 ,
,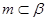 ,给出下列四个命题:
,给出下列四个命题: ∥
∥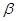 ,则
,则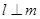 ;
;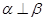 ,则
,则 ∥
∥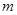 ;
;