题目内容
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为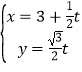 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
【答案】
(1)
x2+(y![]() )2=3
)2=3
(2)
(3,0)
【解析】(1)由 ρ =2![]() sin θ , 得 ρ2 =2
sin θ , 得 ρ2 =2![]() ρ sin θ,
ρ sin θ,
从而有. x2+y2=2 ![]() y, 所以x2+(y-
y, 所以x2+(y-![]() )2=3
)2=3
(2)设P(3+ ![]() t,
t, ![]() t), 又C(0,
t), 又C(0, ![]() ),则|PC|=
),则|PC|= ![]() =
= ![]() ,
,
故当t=0时,|PC|取最小值,此时P点的直角坐标为(3,0).
【考点精析】解答此题的关键在于理解极坐标系的相关知识,掌握平面内取一个定点O,叫做极点;自极点O引一条射线OX叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系,以及对直线的参数方程的理解,了解经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为 (
(![]() 为参数).
为参数).

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案【题目】(2015·陕西)随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
【题目】(2015·陕西)随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(1)从该班随机选1名同学,求该同学至少参加一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1 , A2 , A3 , A4 , A5 , 3名女同学B1 , B2 , B3 . 现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.


